平面図形 辺の比と面積の比 前田昌宏の中学受験が楽しくなる算数塾
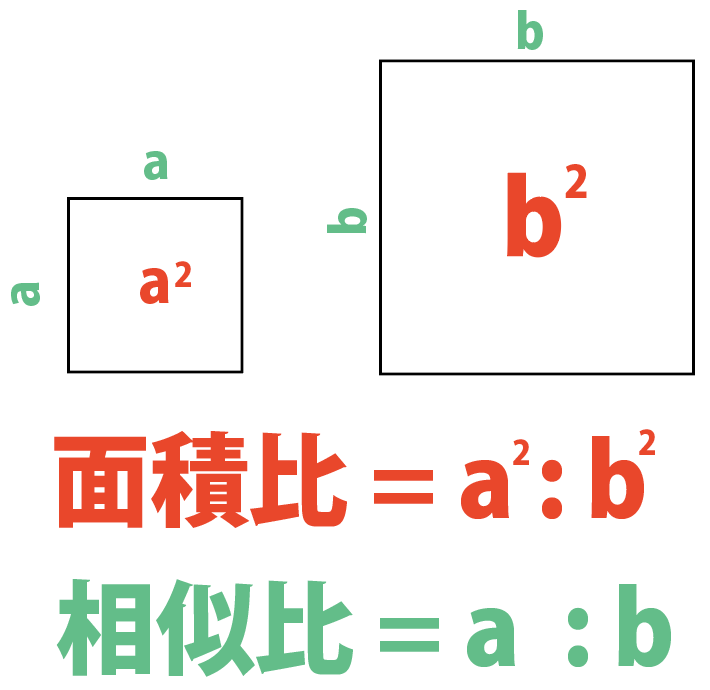
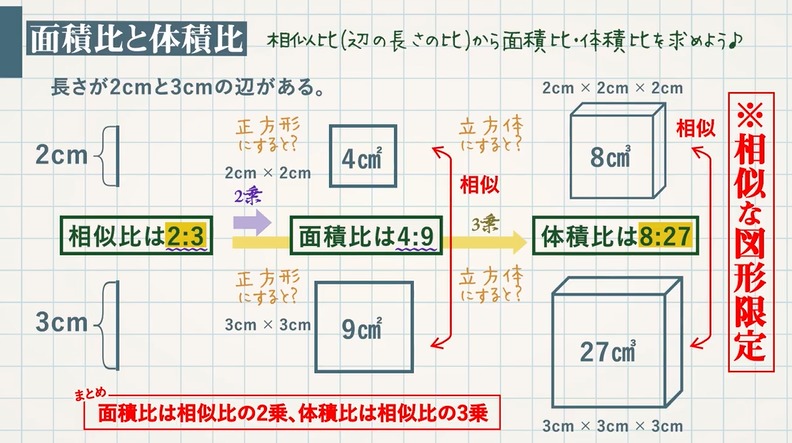
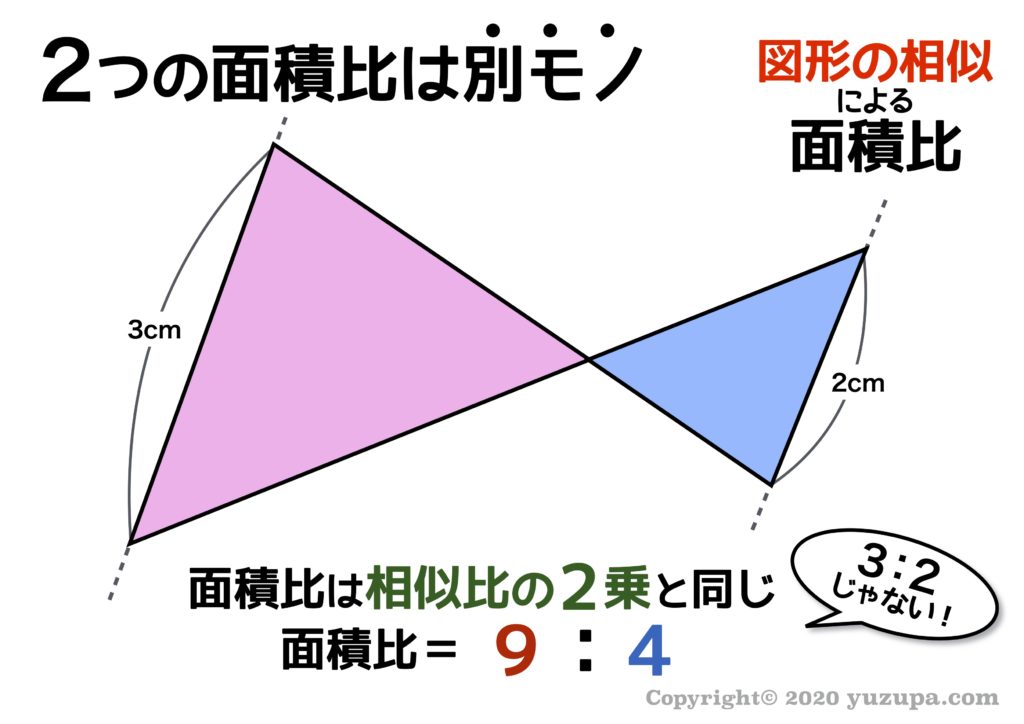
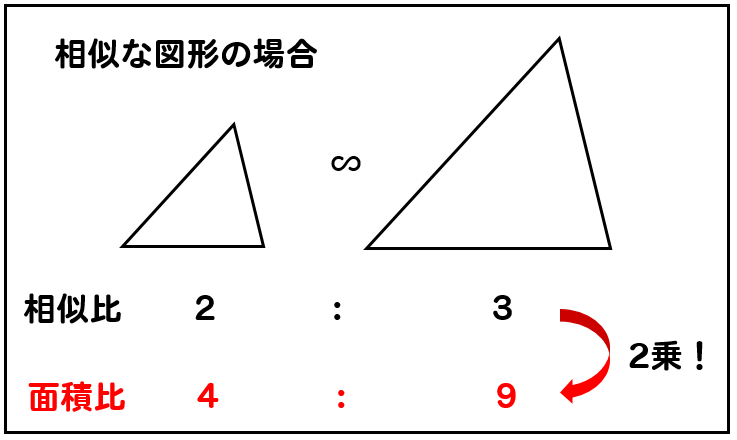
相似比(辺の長さの比)から 面積比 と 体積比 を求めましょう。 長さ $2\rm cm$ と $3\rm cm$ の辺があります。この $2$ 辺の長さの比 (相似比)は $\textcolor{blue}{23}$ になります。 正方形にしてそれぞれの面積を考えると、 $1$ 辺の長さが $2 \rm cm2×2(2\textcolor{blue} つまり、辺の長さの比(相似比)の3乗の比が体積比に相当することを理解しておきましょう。 円錐の体積比の計算問題を解いてみよう それでは、塩水の相似比、面積比、体積比の算出に慣れるためにも、練習問題を解いていきましょう。 例題
相似 辺の比 面積比
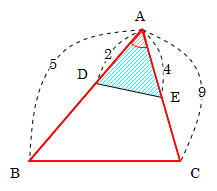
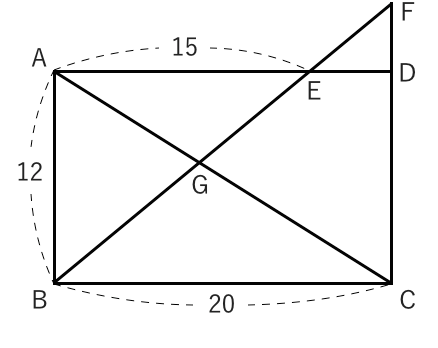
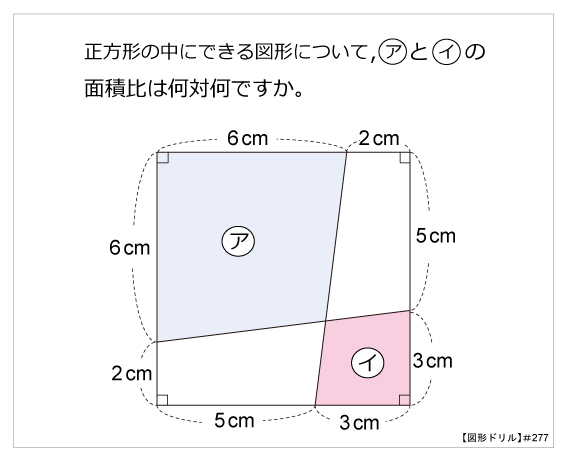
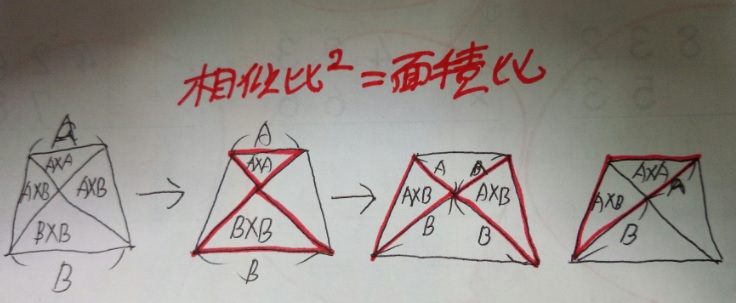
相似 辺の比 面積比-ここで、 長方形の面積を1とします。 ・・・ 1にする。というのは、 仕事算でも使う魔法の言葉 ですw Aの縦辺の長さが1なので、Aの横辺の長さは $(面積)なので 面積の比は \ (a×ab×b\) となるわけです。 もちろん、三角形だけで 面積の比はその共通角をはさむ2辺の積、 三角形ABCの面積:三角形ADEの面積=5×9:2×4=45:8 で求められるというものです。 この解き方を習っている場合は、 ア×3:イ×2=2:1 な

平面図形をマスター 三角形の面積比 応用編その2
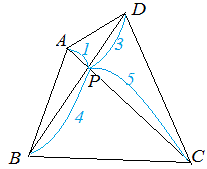
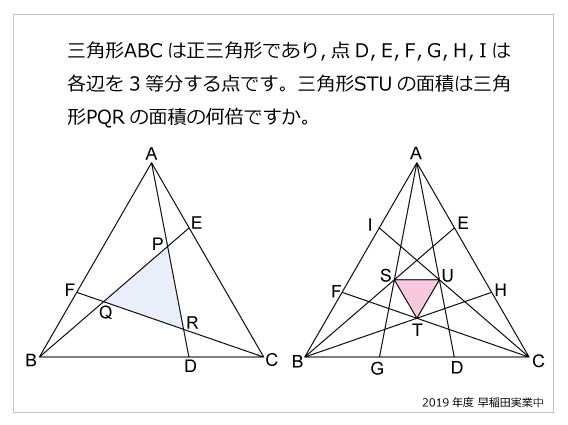
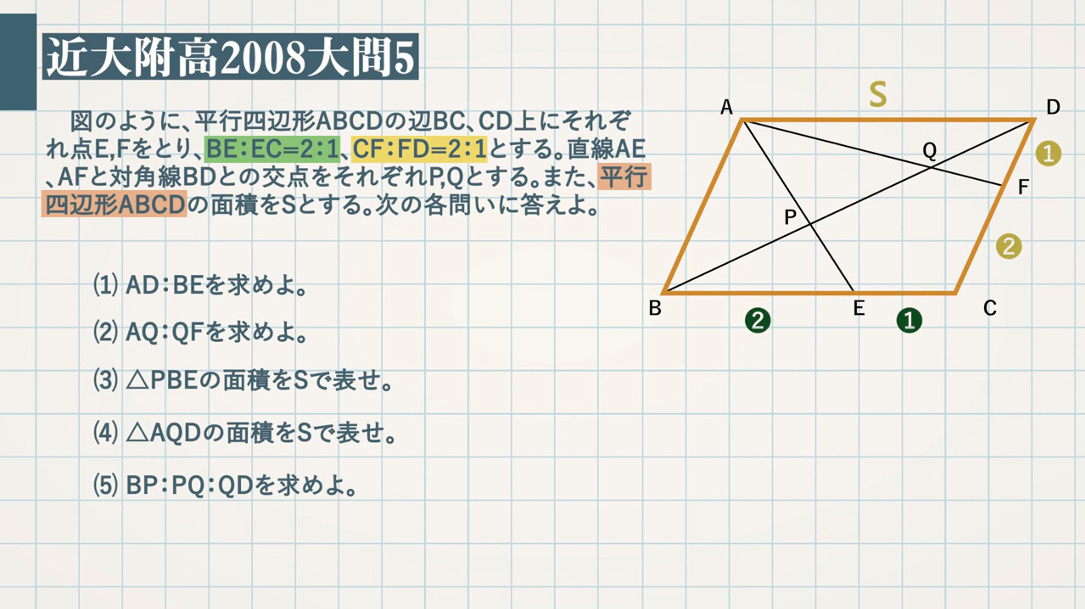
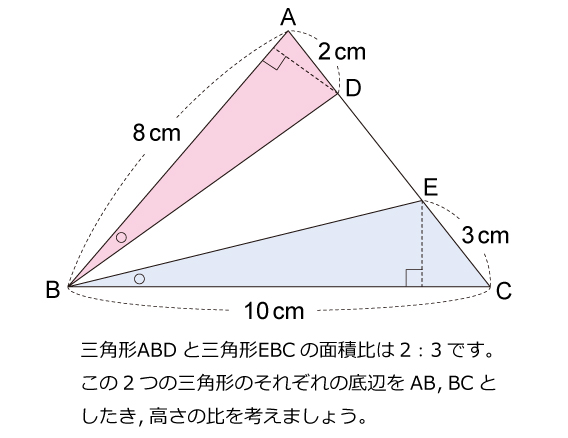
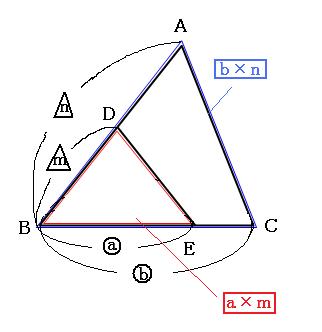
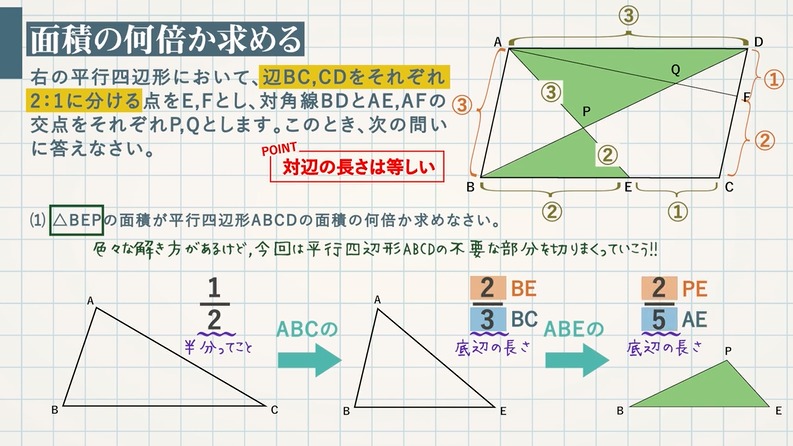
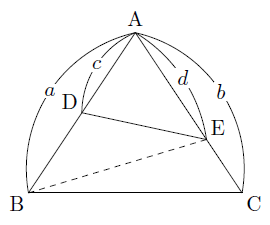
一辺を共有する三角形の面積比の公式 公式1 図において ABP ABP ACP=BDCD ACP = BD C D 証明 ABP ABP ACP= ACP = ABD ABD ACD=BDCD AC D = BD C D 「一辺を共有する三角形の面積比は線分の比に変換できる」 と覚えておきましょう。 代表的な応用例としては, チェバの定理 の証明が挙げられます。 角を共有する三角形の面積比の公式 公式2 図において ABC ABC ADE=AB\times 三角形の面積は通常だと、 (底辺) × × (高さ) ÷2 = ÷ 2 = (面積) と計算します。 しかし三角比があれば、面積の公式によって、 2辺とその間の角から面積を計算 できるようになります。 今回はこの 三角形の面積の公式 を解説していきます! トムソン 面積の公式を使えるようになりたいな 他の面積の公式も知りたい 面積の公式の証明したい! そんな疑問にお答えしていきます! いろいろな三角形の面積を比較しながら、最終的な面積の比較にもっていきます。 三角形pqr の辺の延長線上で、比がわかっている bq : qr : rf = 2 : 2 : 1 に注目します。 次に、cr : rp : pd = 2 : 2 : 1 に注目して、
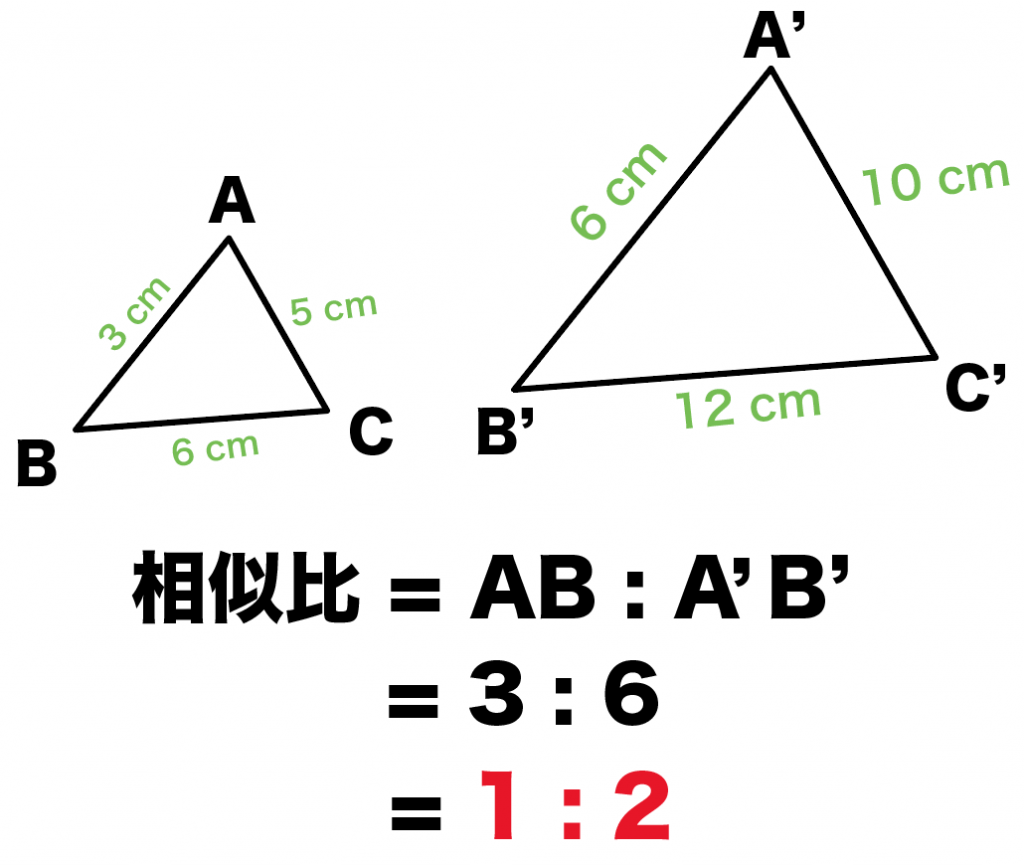
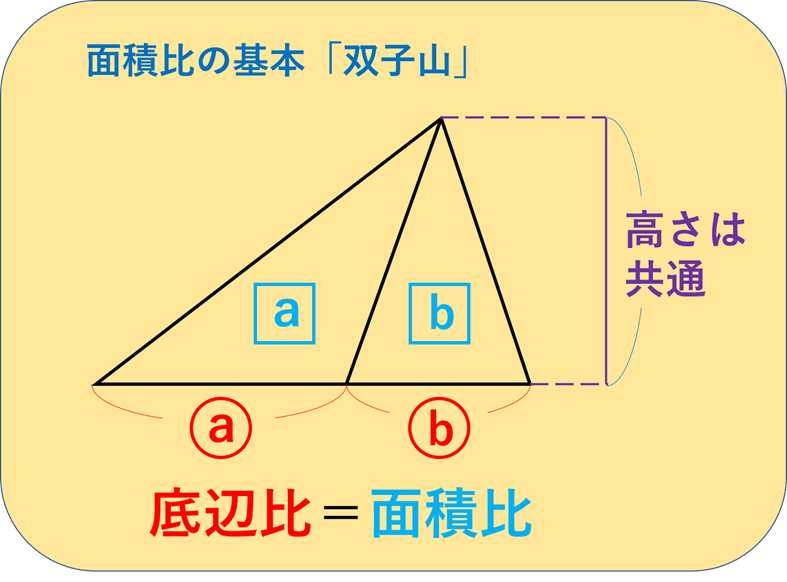
以上のことから、三角形の面積比を考える場合、「 (底辺の比)×(高さの比)=面積の比 」となることがわかります。 まとめ ここまでが三角形の面積比の基礎部分と言えます。 ただ,問1,問2(1)は,簡単な証明など,定期テスト対策に丁度良いので,早めに解いてみても良いかもしれません。 過去に紹介した似た問題は, これ や これ ですね。 title:辺の比・面積比・相似 範囲:中3相似 出典:16年度 東京都 高校入試 数学 過去問 平行線と線分の比の問題の解き方がわかる3ステップ こんにちは!ぺーたーだよ。 相似の単元では、 相似条件とか、 相似の証明とか、いろいろ勉強してきたね。 今日は ちょっと新しい、 平行線と線分の比のから辺の長さを求める問題 について解説して
相似 辺の比 面積比のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  | |
「相似 辺の比 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「相似 辺の比 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「相似 辺の比 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「相似 辺の比 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「相似 辺の比 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「相似 辺の比 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「相似 辺の比 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「相似 辺の比 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「相似 辺の比 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「相似 辺の比 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「相似 辺の比 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
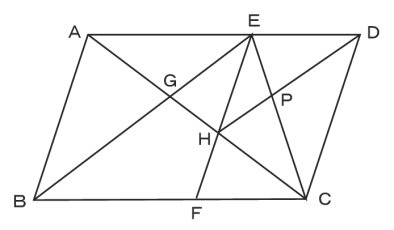
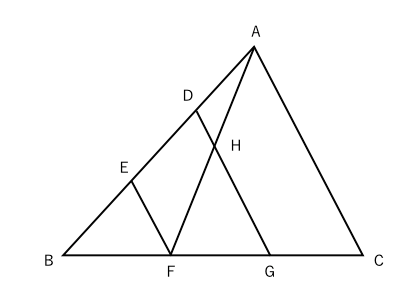
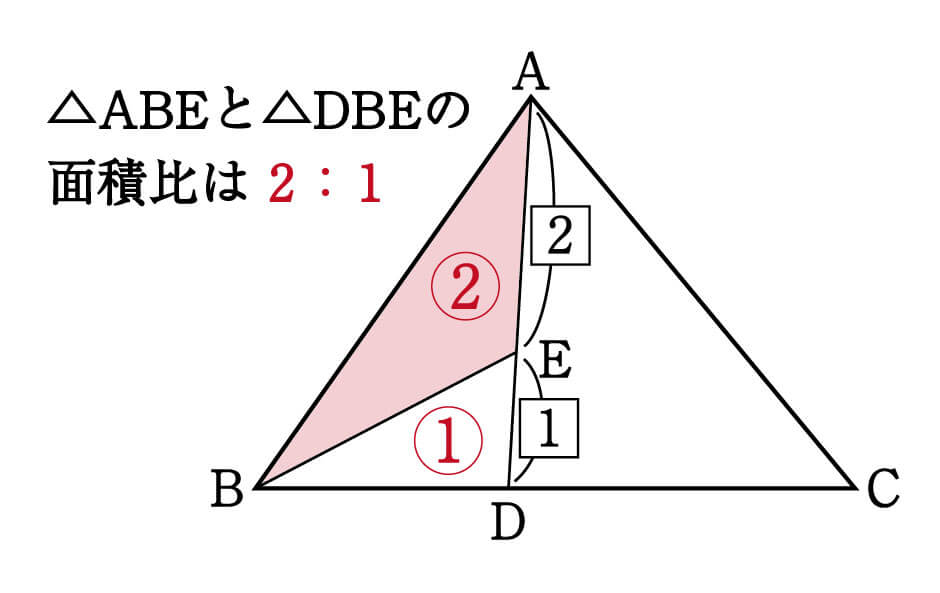
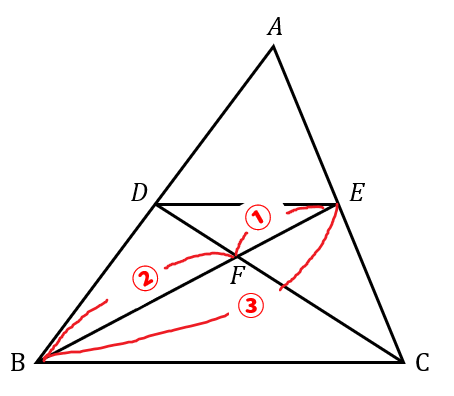
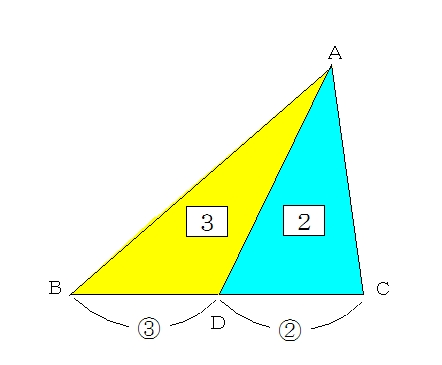
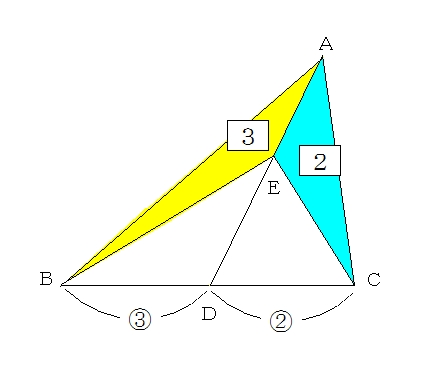
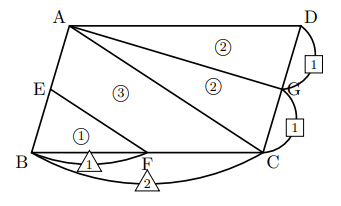
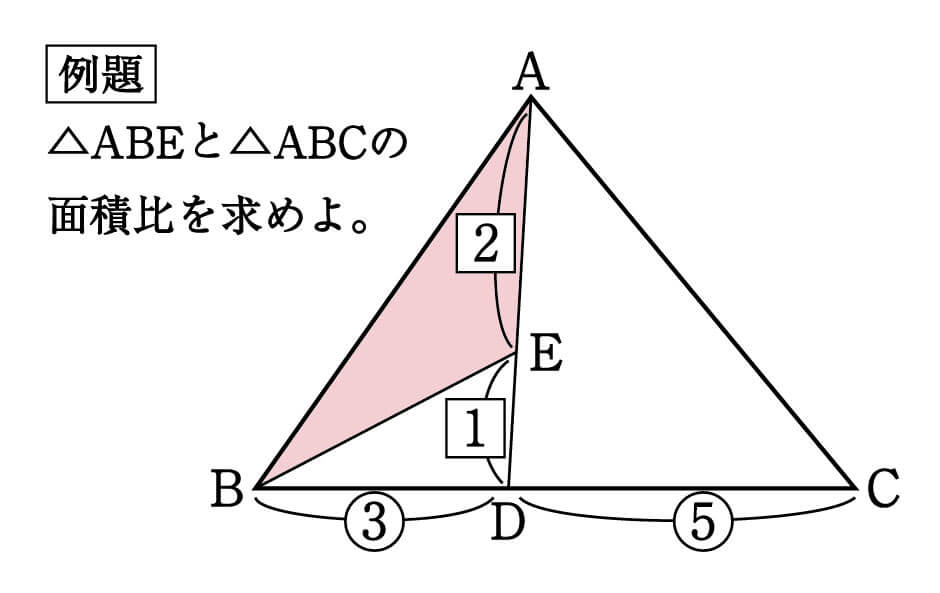
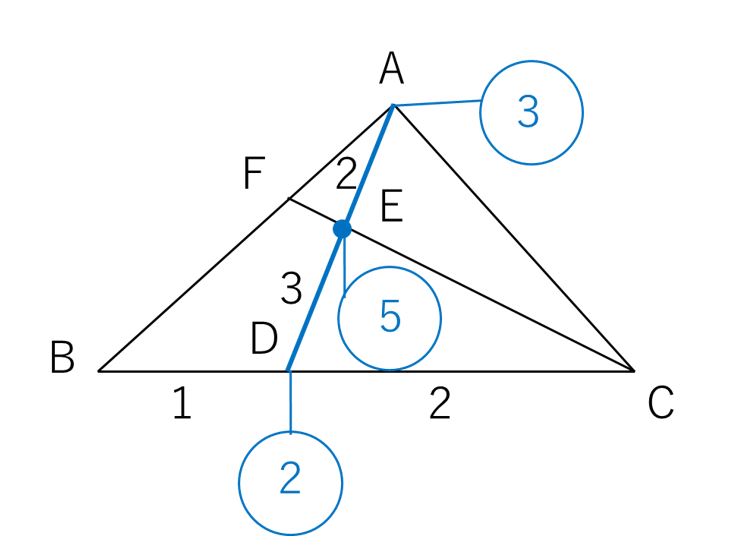
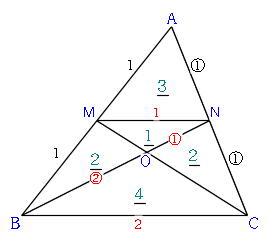
三角形の左側に注目すると、 ABEと BDEは「高さが同じ隣り合う三角形」であることがわかります。 ①の型に該当するので、2つの面積比は底辺比に等しい。 つまり ABE: BDE=2:1となるわけです。 続いて、 ABDと ACDを見てみると、こちらも①の型に当てはまります。 ABDの面積を、 ABEと BDEを合わせて3とした場合、 ABDと ACDの面積比は、底辺の比が3:5なので 正しい考え方 一度、「 面積が同じ長方形の場合、縦辺の長さの比と、横辺の長さの比は 逆比 となる。 」事を 忘れてみましょう!
Incoming Term: 面積比 辺の比, 三角形 面積比 辺の比, 辺の比 面積比 二乗, 相似 辺の比 面積比,




0 件のコメント:
コメントを投稿