算法思想 首先判断其两边之和是否大于第三边,若大于则判断可以构成三角形,再进一步判断该三角形是什么三角形,并计算这个三角形的面积;否则不能构成三角形。 ① 从键盘输入三角形的三条边。 ② 判断两边之和是否大于第三边。 ③ 若条件成立则直角三角形计算器 如果给出足够的几何属性, 直角三角形计算器 就能自动补全直角三角形的所有属性,如面积,周长,边和角度。 直角三角形是一个具有三个顶点(角)和三个边(边)的多边形,其中两条边以直角相交。 直角三角形 维基百科页面如何计算三角形角度。 直角三角形公式 计算角度 43;

Unity3d引擎 2d游戏自动瞄准算法实现 Weixin 的博客 程序员信息网 程序员信息网
三角形角度算法
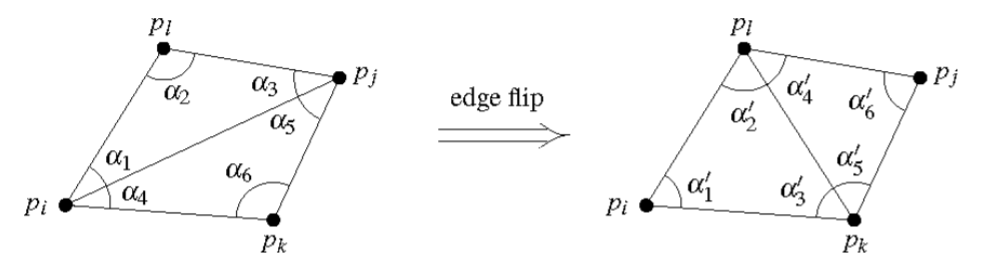
三角形角度算法- Delaunay 剖分是一种三角剖分的标准,实现它有多种算法。 本次采用 BowyerWatson 算法,算法的基本步骤是: (1)构造一个超级三角形,包含所有散点,放入三角形链表。 (2)将点集中的散点依次插入,在三角形链表中找出其外接圆包含 插入点的三角形(称为 3最优性:任意两个相邻三角形形成的凸四边形的对角线互换,两个三角形最小的角度不会变大。 4区域性:新增、删除、移动某一个顶点时只会影响临近的三角形。 5凸包:三角网最外层的边界形成一个凸多边形的外壳。 23 一种Delaunay的构造过程——逐点插入法 Delaunay剖分是一种三角剖




三角形角度算法三角形角度計算公式知道三條邊長 求任意角度 作業幫翻譯此網頁 Laniwendt
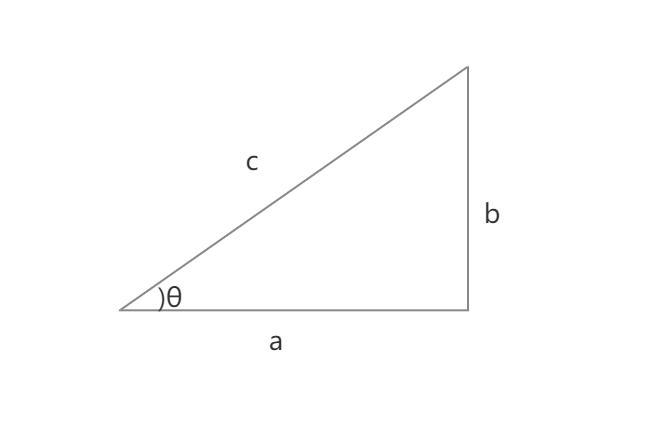
如果三角形直角边的边长是3和4,并且你让a = 3,b = 4,则可得到等式:32 42 = c2。 求a和b的平方。一个数的平方等于它和自己相乘,即a2 = a x a。算出a和b的平方,将它写入你的公式中。 如果a = 3,则a2 = 3 x 3,即9。如果b = 4,则b2 = 4 x 4,即16。 将以上值代入等式,可得出:9 16 = c2。 求c2的平方根 三角函数 1 角度和弧度的转换: radians = degrees * PI / 180 degrees = radians * 180 / PI 2 非直角三角形的计算: 已知a,b,和角度theta c,则有:c2 = a2 b2 2ab*cos(theta c) 3 三角函数图: 有公式: a / sin(the以下我们介绍ZBuffer算法,主要有2步。 1 ZBuffer算法需要为每个像素点维持一个深度数组记为zbuffer,其每个位置初始值置为无穷大(即离摄像机无穷远)。 2 随后我们遍历每个三角形面上的每一个像素点 x,y,如果该像素点的深度值z,小于zbuffer x,y中的值
已知三角形边长,计算三角形的角度过程如下: 1、设三角形中角A所对应的边长是a,角B所对应的边长是b,角C所对应的边长是c。 再利用公式: ①CosA= (c^2b^2a^2)/2bc ②CosB= (a^2c^2b^2)/2ac ③CosC= (a^2b^2c^2)/2ab 算出每一个角的余弦值,利用计算器上的反余弦函数求直角三角形的角度 从已知两边求角度 若我们知道 直角三角形 两条边的长度,我们便可以求三角形的未知角度。 例子 梯子搁在墙上,如图。 梯子与墙之间的 角度 是多少? 我们可以用 正弦、余弦或正切来做! 但应该用哪个呢? 我们可以这样做: 一、看看已知的边是 邻边(就是:我们想求 利用CORDIC算法计算三角函数 利用CORDIC算法计算cos和sin值,利用了坐标在在圆上旋转的特性,用坐标值表示cos和sin,核心思想是把乘法运算转换成移位运算 这里主要先介绍如何利用CORDIC算法计算固定角度 ϕ 的 c o s ( ϕ) 、 s i n ( ϕ) 值。 一般利用MATLAB计算三角
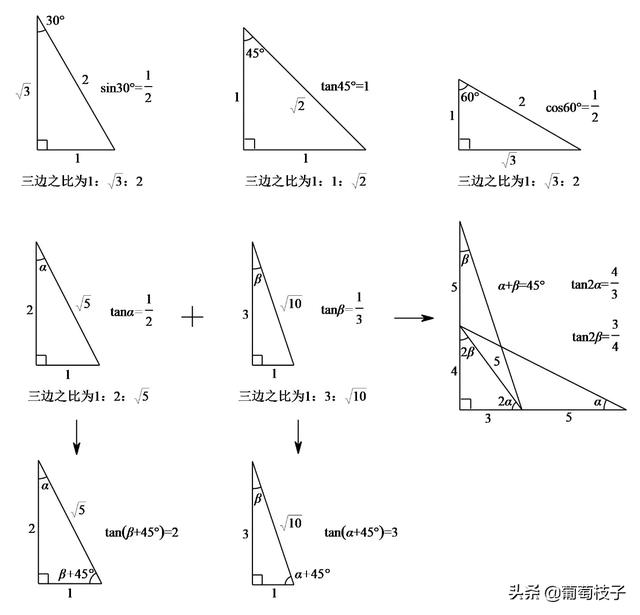
1) 有两角为 60° 的三角形为等边三角形; 2) 等腰三角形底边对应的的高、中线与角平分线重合; 3) 有一角为 45° 的直角三角形为等腰三角形; 4) 勾股定理。 更多特殊角度的三角函数精确值算法见 1。 对于一般的角度\ (~x\),可用 Taylor 公式 2 算出任意精度点击公众号"计算机视觉life"关注,置顶星标更快接收消息! 本文编程练习框架及数据获取方法见文末获取方式 菜单栏点击"知识星球"查看「从零开始学习SLAM」一起学习交流小白:师兄,师兄,你在《 从Delaunay 三角剖分是三角剖分中所有三角形最小角度的最大化,倾向于避免狭长的三角形出现。由于 Boris Delaunay 从 1934 年开始研究这个课题,因此这种三角剖分是以 Boris Delaunay 的名字进行命名。 对于同一直线上的一组点,不存在 Delaunay 三角剖分;同一圆上的四个或多个点,存在不唯一的 Delaunay 三角




Vivado中cordic Ip核使用 计算正余弦 Sin Cos 爱代码




Verilog实现基于cordic算法的双曲函数计算 程序员大本营
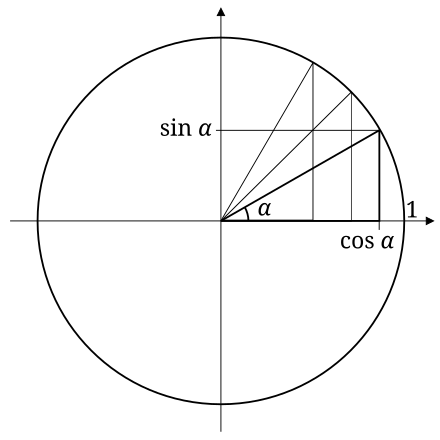
三角函數(英語: Trigonometric functions )是數學中常見的一類關於角度的函數。 三角函數將直角三角形的內角和它的兩個邊的比值相關聯,也可以等價地用與單位圓有關的各種線段的長度來定義。 三角函數在研究三角形和圓等幾何形狀的性質時有重要作用,也是研究振動、波、天體運動以及基于三角网格寻路算法的运作原理我已经在上一篇日志中讲到了,在这里不再赘述,直接进入主题——Delaunay三角剖分的实现(By AS3)。 首先我们来定义数据类型。 我需要一个接口和两个类来分别表示点(角)、边和三角形这三个概念,其中由于点是需要使用 本文以几何角度,理解线性变换中的矩阵,能帮助学习者对其建立直观音箱。 老齐 空间中判断点在三角形内算法(方程法) 三维空间中判断点在三角形内外的算法与平面中有所不同,《平面中判断点在三角形内算法(同向法)》中提到的算法在三维空间中已经无法生效,也很难利用上。一个最简单的




如何计算角度 8 步骤 包含图片



实现简易gpu光栅器 一 知乎
如何使用Javascript Math库计算直角三角形的角度? js 关于三角函数算法 弧度 和 角度的理解, 以及相互转换 角的两种单位 度 和 弧 1、弧度的定义 我们知道"度"的定义是,"两条射线从圆心向圆周射出,形成一个夹角和夹角正对的一段弧。当这段弧长正好等于圆周长的360分之一时,两条射 3D三角形网格补洞算法及源码 (转) 在逆向工程中,由于设备或模型的原因,我们获取得到的三维模型数据往往并不完整,从而使得生成的网格模型存在孔洞,这对后续的模型分析会造成影响。 下面介绍一种基于径向基函数(RBF:Radial Basis Function)的三角网格补如果给出足够的几何属性,任意三角形计算器就能自动补全任意三角形的所有属性,例如面积,周长,边和角度。 三角形是具有三个顶点(角)和三条边(边)的多边形。 任意三角形 维基百科页面相关计算器:等边三角形计算器等腰三角形计算器直角三角形计算器



鏡頭視角的計算及應用




直角三角形邊長求角度直角三角形 Itha
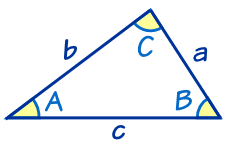
如果已知三角形的三条边a、b、c,三个角α、β、γ,可以由余弦定理得到三角形的三个内角: 1、α角的角度 2、β角的角度 3、γ角的角度 余弦定理的含义是对于任意三角形,任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍 恰当的改变三角形三个顶点的调用顺序就可以得到方向一致的有向线段,分 为以下6 种顶点顺序,如图210 和图211 所示: 种情况图210 顶点顺序1 (面法向量指向外面) 种情况图211 顶点顺序2 (面法向量指向外面) 中国科学技术大学本科毕业论文 15 设三角形从生长过程角度,三角网生长算法分为收缩生长算法和扩张生长算法两类。 收缩生长算法是先形成整个数据域的数据边界(凸壳),并以此作为源头,逐步缩小以形成整个三角网。 扩张生长算法与收缩算法过程刚好相反,是从一个三角形开始向外层层扩展,形成覆盖整个区域的三角 52tin的建立 第55




三角形角度算法三角形角度計算公式知道三條邊長 求任意角度 作業幫翻譯此網頁 Laniwendt



1
概述图形化解释1 超级三角形插入第一个点2 插入第二个点概述本人还有一些细节没理清,所以希望大家多多交流了解定义什么是Delaunay三角大家可以看其他博客,写的很清楚了。这里主要说一下怎么实现的 判断方法三角形是不是Delaunay三角形很简单,这个三角形做外接圆,外接圆内或者 本篇文章所讲述如何实现mesh减面工具。思想由作者创建。目录1、Unity Mesh对象里的数据构成2、智能减面详解Unity Mesh对象里的数据构成 这里主要介绍相关的数据,如下图。 Triangles数组存储的是所有三角形对应于vertices数组里的顶点,triangles从坐标0~n依次存储了每个三角形三个顶点在vertices下的位置等腰三角形计算器 如果给出足够的几何属性, 等腰三角计算器 就能自动补全等腰三角形的所有属性,例如面积,周长,边长和角度。 等腰三角形是具有三个顶点(角)和三个边(三边)的多边形,其中两条边长度相等。 等腰三角形 维基百科页面




如何使用opencv进行delaunay三角剖分和voronoi图 图像算法imalg的博客 程序员信息网 Gettrianglelist 程序员信息网



三角形怎么算边长图解 第1页 要无忧健康图库
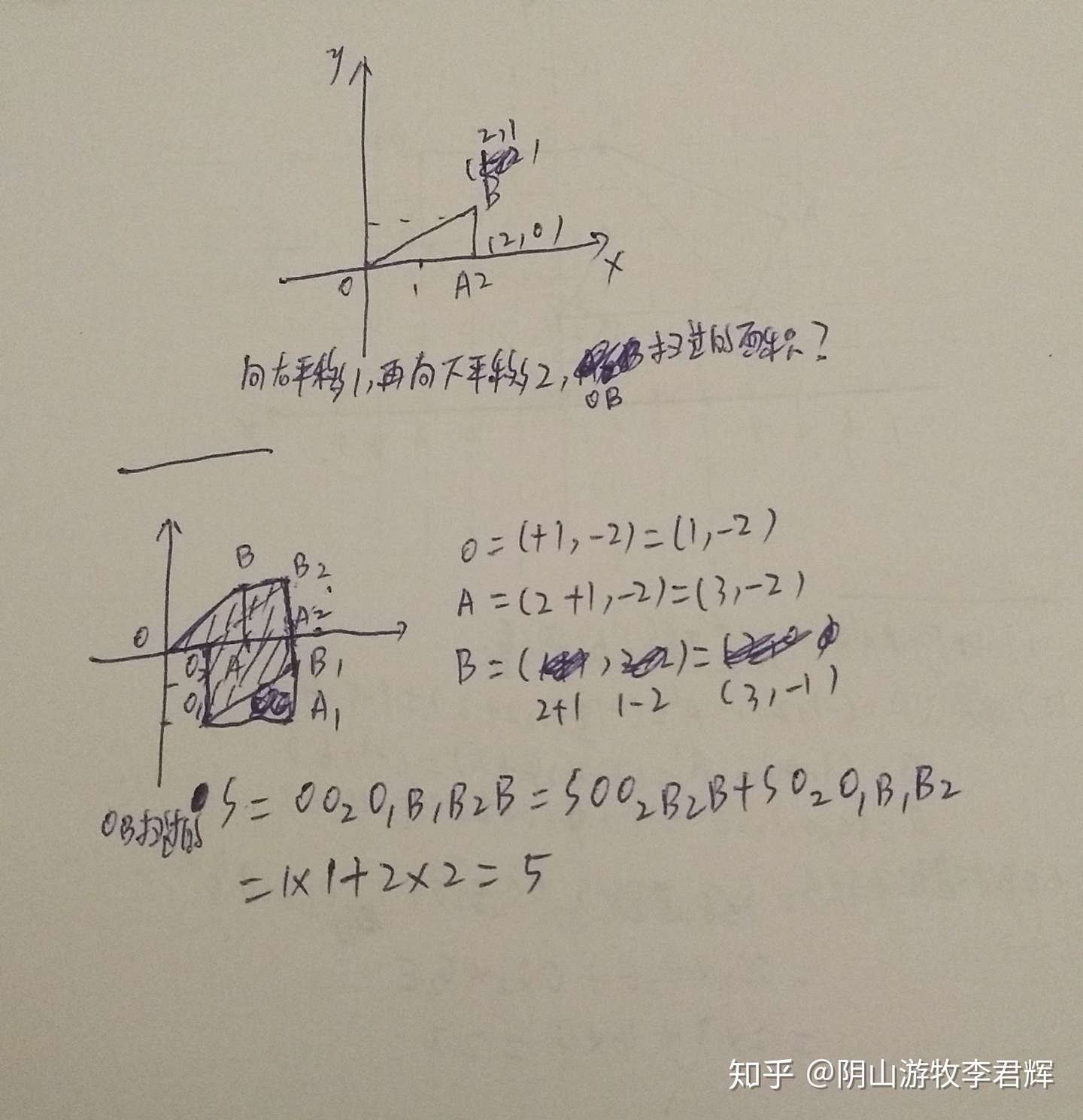
直角三角形斜边有普遍的计算公式算法,也有特殊角度的简易算法,本篇重点介绍直角三角形斜边斜边的几种计算方式和步骤。 工具/原料 more 纸 笔 方法/步骤 1 /5 分步阅读 明确定义。 直角三角形斜边是指直角对应的对边,也是直角三角形中最长的边。直角三角形斜边和其他两条边形成的夹角之更多类似问题 > 为你推荐: 特别推荐 神舟13号宇航员到了!神舟十四号 输入三角形的三边长,计算三角形的面积,结果保留两位小数。 边长分别为a,b,c,三角形的面积公式为s=sqrt(p(pa)(pb)(pc)),其中p=(abc)/2。 2 输入说明 输入格式:共一行,输入三个数,保留两位小数,用空格隔开各个数据。 3 输出说明



樓梯角度算法樓梯的各種尺寸要求及公式匯總 請收好 Xvleq
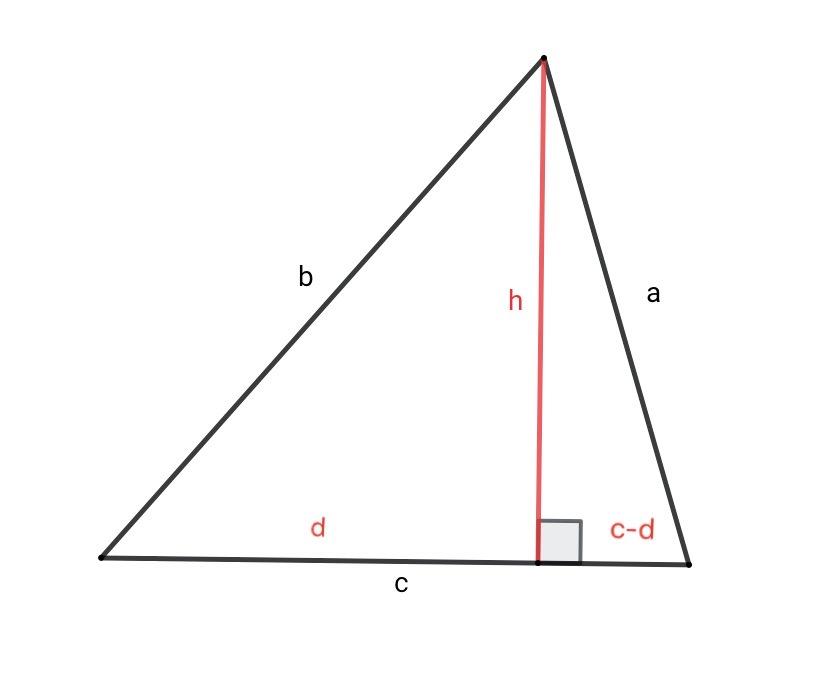



三角形面积公式 知乎
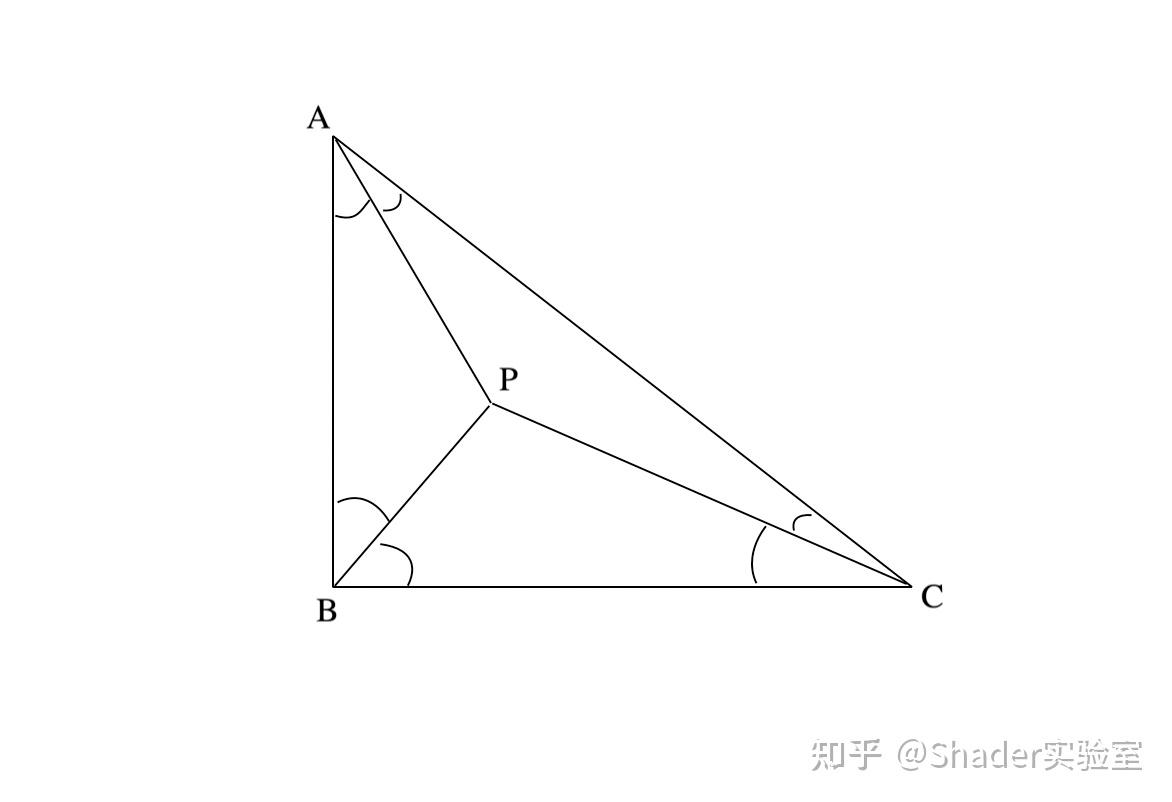
这个图形里面出现了以下角度: 18°角: , 36°角(18°的2倍角): 72°角(18°的4倍角): , 90°角(18°的5倍角): , 显然, 是一个等腰三角形,CA=CB。 CO是底边AB的中垂线,OA=OB。 只要我们能算出 的 底边AB 和两腰CA、CB的长度之比,就能立即得出 sin18° 和 sin72°,再利用三角函数的性




如何计算角度 8 步骤 包含图片



少有人走的路 一步一步实现多尺度多角度的形状匹配算法 C 版本



直角三角形邊長求角度直角三角形 Itha




Pagerank 基本算法 Great Power Law



解三角形




计算另外两个角度之间的角度
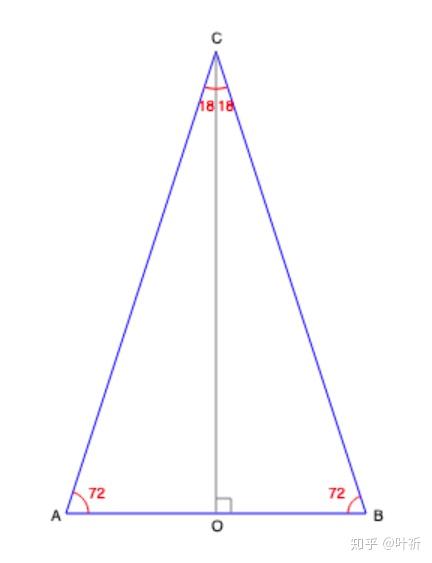



18 倍角的三角函数计算方法 几何算法 知乎



等腰三角形面积算法 吾爱中考网



乘法算法格子乘法网格法乘法 蜂窝格子png剪贴画角度 白色 文本 免抠素材下载 图片id 其它元素 Png素材 素材宝scbao Com



勾股定理知识回顾 广州北北电子科技有限公司




圖形長度和角度算法 請前輩幫忙 Mobile01
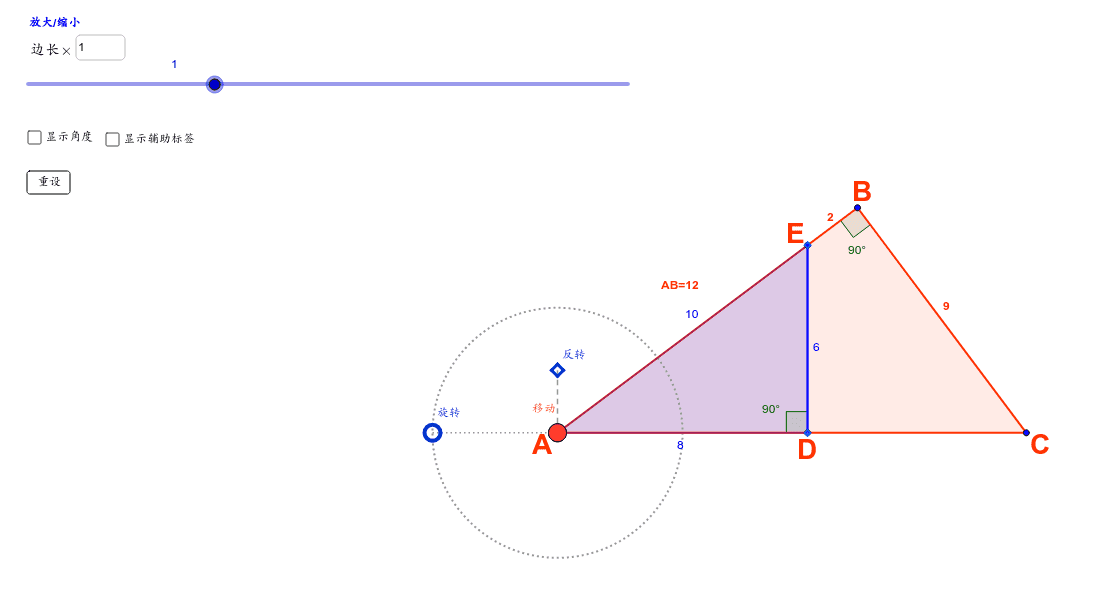



相似三角形 任务4 Geogebra
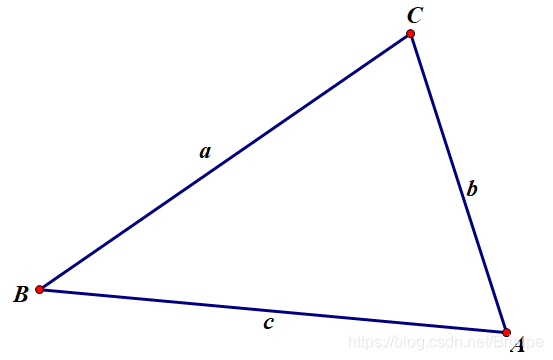



各种三角形边长的计算公式 We Are All In The Gutter But Some Of Us Are Looking At The Stars Csdn博客 三角形边长




关于算法 计算圆与三角形的相交面积 码农家园




趣味初中几何题 还记得不




从这个角度去理解数据结构与算法更容易 Mbe1b0的技术博客 51cto博客
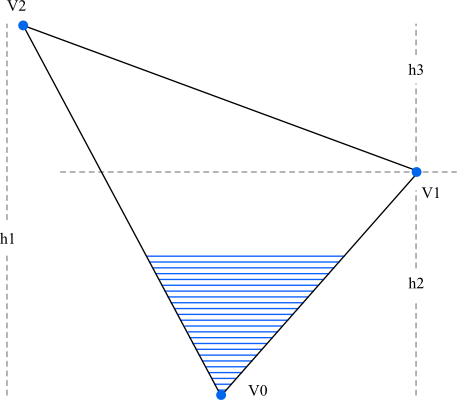



Github Tinyrenderer渲染器课程实践记录 三角形光栅化 Fijiisland 博客园



蜻蜓大脑算法速度超快 Ai科学家 拿来吧你 591资讯




直角三角形知道两边求角度 中考数学专题复习 直角三角形 雪灵谷自然地理的博客 Csdn博客



计算三角形角度 西瓜视频搜索



1



三角角度公式图 第1页 要无忧健康图库




Unity3d引擎 2d游戏自动瞄准算法实现 Weixin 的博客 程序员信息网 程序员信息网




基于verilog的cordic算法实现 Wx612b5b677de的技术博客 51cto博客




距离差分矩阵ddm算法 我的blog屋 程序员its404 程序员its404



Cos相似度算法余弦距离计算 工程师小哥的博客 程序员宅基地 Cos距离公式 程序员宅基地



计算三角形角度 西瓜视频搜索



计算几何 Delaunay 三角化算法原理与实现 稷殿下




计算几何课程实验总结报告chazelle 2 中的算法其中将平面内的点和直线按一定关系转化为相应




正弦 余弦和正切



三角函數基本概念




静态条件下三轴加速度求角度的算法 搜索编程资料 就到琅嬛玉洞




关于算法 计算圆与三角形的相交面积 码农家园




三角形面积的五种典型算法 简书




三角学 维基百科 自由的百科全书



直角三形角度公式图 第1页 要无忧健康图库




三角形求面积的五种算法答案 简书



1



特殊直角三角形 Wikiwand




直角三角形只知道一条边 直角三角形知道一条边长和一个角度 怎么计算出另外两条边的长度 三人行教育网 Www 3rxing Org



三角形的角度 中 知乎



基于三角形相似定理的角度检测算法专利 专利查询 天眼查




如何求角的度數已知三邊長 求任意一個角度 直角三角形 Mspk



计算三角形角度 西瓜视频搜索




這題求算法 Clearnote




觀念 等腰三角形 求頂角角度 Youtube




3种方法来计算三角形的周长




如何计算角度 8 步骤 包含图片



使用cordic算法求解角度正余弦及verilog实现 比较懒 博客园



对角线安装的双舵轮运动模型 Ylp Blog



三角角度公式图 第1页 要无忧健康图库




机器视觉算法与应用 测量锯齿的角度 Sinat 2761的博客 程序员宝宝 程序员宝宝



计算三角形角度 西瓜视频搜索




直角三角形邊長求角度直角三角形 Itha




如何计算角度 8 步骤 包含图片




三角形面積公式 兩邊一夾角 Youtube




三角形角度算法 Mdsulja




Ruppert S Algorithm 曹玮 金逸飞 沈彤 算法简介 Delauney三角化实现了质量很高的点集三角化 但是 特定的输入会造成三角化的结果包含很多形状较细的三角形 如左图 在这种情况下 一般采用加点的方法 使得三角化结果较为均匀 如右图 这样的




三角形 08 直角三角形內角的基本計算題2 Youtube




如何算等边三角形的顶角角度 已知高度和底边长度 雨露学习互助



三角函数 已知直角三角形的斜边长度和一个锐角角度 求另外两条直角边的长度 掘金




基礎 直角三角形斜邊上的高與線段長 Youtube




面基算法數學科知識園地 Dgekn



達人專欄 一篇文弄懂三角函數 其實它真的不可怕 Johnny的創作 巴哈姆特



問題回覆 已知直角三角形兩邊 求斜邊及夾角 Labview Plc還未出師的小工程師部落格 痞客邦
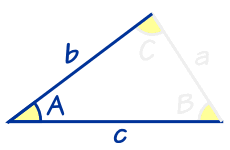



解sas 三角形




3d游戏之投影矩阵算法技术实现 海洋个人博客 程序员资料 3d投影算法 程序员资料




Cordic算法 一 圆周旋转模式下计算三角函数和模值 龙学焜的专栏 程序员资料 程序员资料
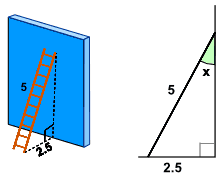



求直角三角形的角度




相贯线多层多道焊轨迹计算与焊道规划 江西上高县捷豹空压机售后 格兰克林空压机



15度角度图解 万图壁纸网



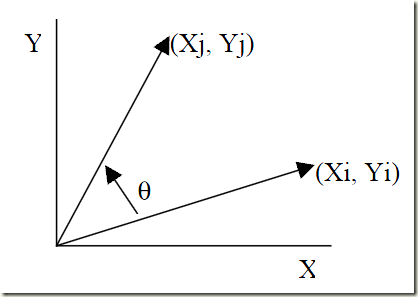
已知三角形三点坐标求角度 中考专题 角系列之坐标系中的特殊角问题 Weixin 的博客 Csdn博客




直角三角形邊長計算機 例 Vny




Python 三角形python小程序 1 計算三角形面積和角度大小 Tzpage



计算三角形角度 西瓜视频搜索
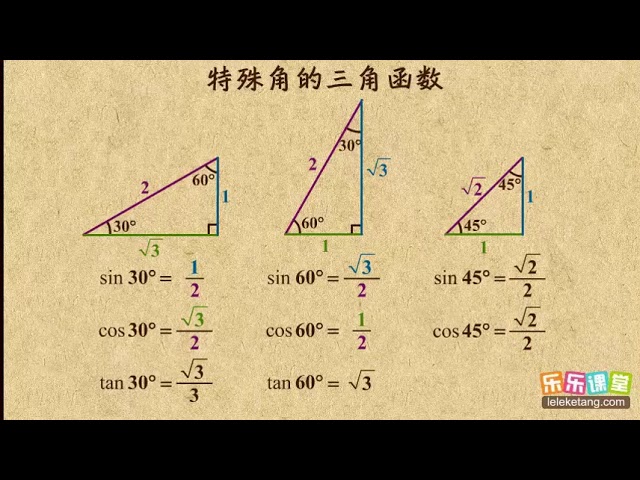



02特殊角的三角函数直角三角形的边角关系初中数学初三 Youtube



勾股定理知识回顾 广州北北电子科技有限公司




直角三角形邊長求角度直角三角形 Itha



1



任意角度计算公式图解 第1页 要无忧健康图库



计算三角形角度 西瓜视频搜索




02三角形按角度分类三角形 1 初中数学初一 Youtube



Welcome澳门威利斯人网站 主頁




如何计算角度 8 步骤 包含图片




初中数学 已知三角形顶角度数和底边长度 求面积 网易公开课
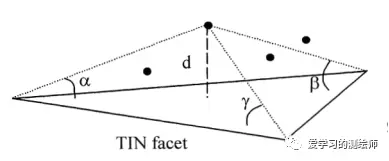



地面点提取算法之 Ptd渐进三角网加密滤波 哔哩哔哩




直角三角形斜边怎么算直角三角形斜边怎么算




等腰三角形已知一个角度和边长 求另一边长度 Segmentfault 思否



三角形怎么算边长图解 第1页 要无忧健康图库



直角三角形三边长度 图片欣赏中心 急不急图文 Jpjww Com




計算機三角函數算法 New North




直角三角形邊長求角度直角三角形 Itha



0 件のコメント:
コメントを投稿