問題 体積の等しい立方体xと球yがあるとき, (1)yはxの頂点をいくつまで内部に含むことができるか? (2)yはxの辺をいくつまで内部に含むことができるか? (大阪大) 空間図形のシンプル難問半径1の2球の和集合の体積 大学入試の過去問 東京大 空間図形 空間図形(球) 空間空間図形~きのこたけのこの体積比べ~ 問題 解説動画 解答きのこの山 アメブロ「身近な数学 問題作り」で日記を公開しています。 中学1年の空間図形に戻る のページの先頭へ ナビゲーション トップページ top page;立体図形の体積と表面積の練習問題 問題1 次の立体の体積を求めなさい。 → 解答 問題2 次の立体の体積を求めなさい。 ただし、この立体は、どの面も(A)のようになっていて、それぞれの穴は反対の面までつきぬけているものとします。 → 解答
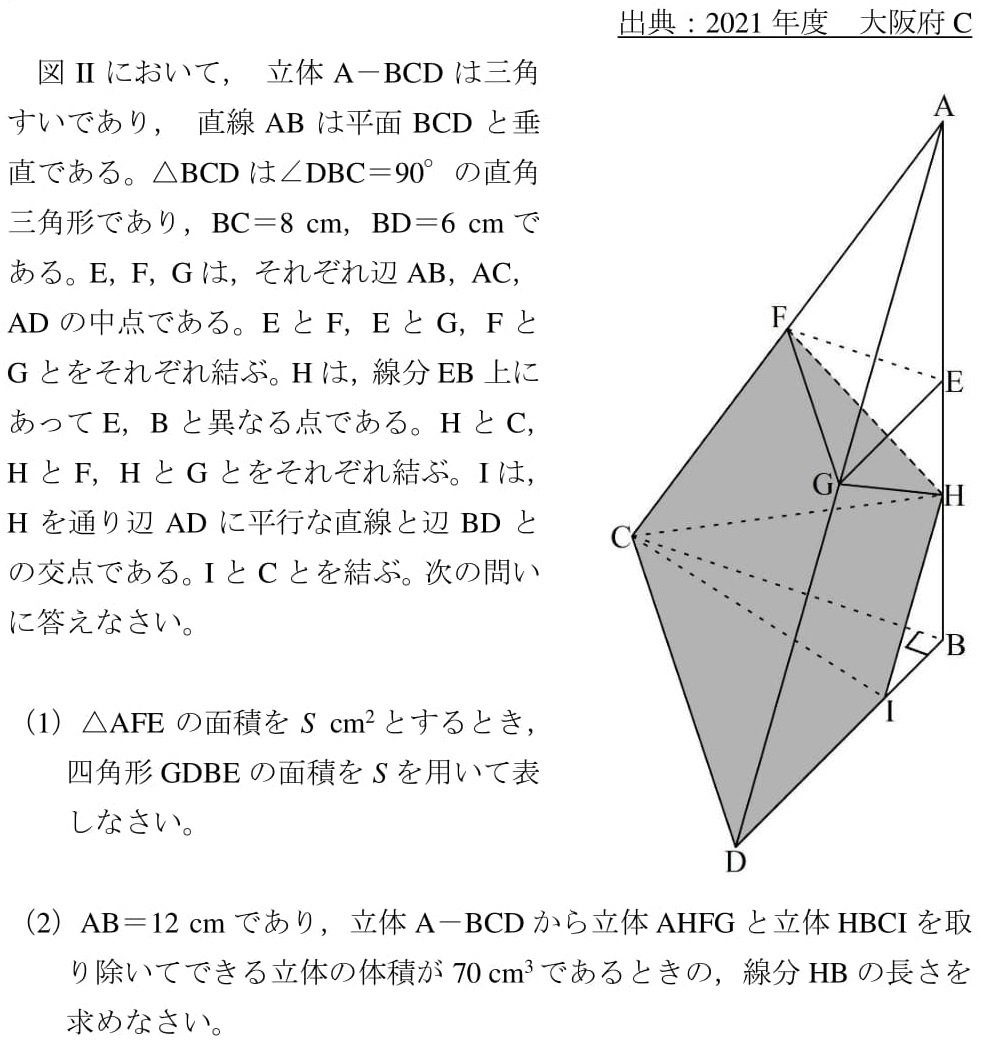
21年大阪府c 相似と面積比 体積比の練習 高校入試 数学 良問 難問
空間図形 体積 問題
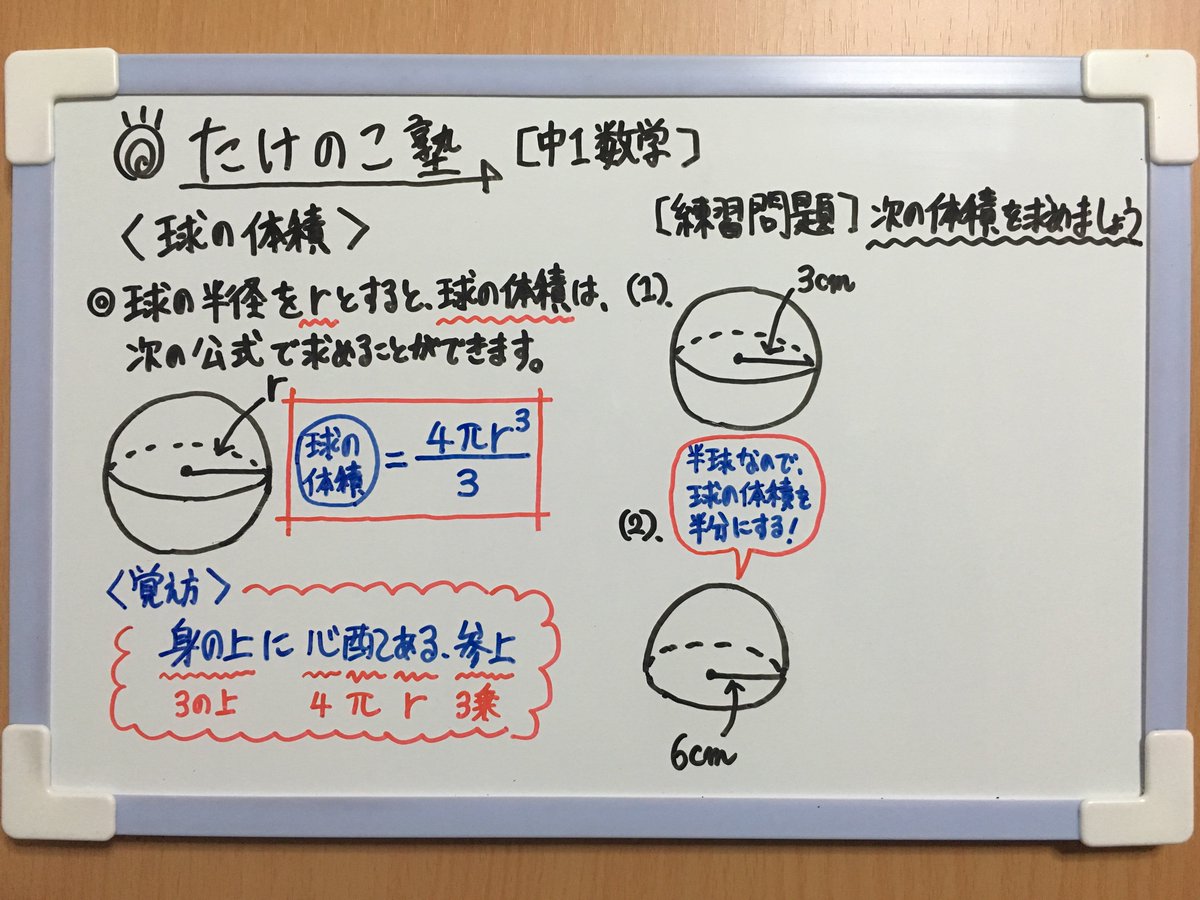
空間図形 体積 問題- 今回は中1で学習する「空間図形」の単元から 球の体積・表面積の求め方について解説していくよ! 球というのは こういったボール状の形をしているものだよね! 実は、ちょっとだけ公式が複雑だったりします(^^;た図形の面積を求めよ。 3 (2)の図形を x軸の周りに1回転させてできる立体の体積 Vを求めよ。 セクション 1 回転軸をまたがる図形 1は三角方程式の解法問題です。 cos2x −cosx = 0 2cos2x −cosx −1 = 0 (2cosx 1)(cosx −1) = 0 cosx = − 1 2 cosx = 1 x = 0,x = 2π 3 ・・・(答)




角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun
中学数学 空間図形の問題 角柱、角すい 直線と直線の位置関係 直線と平面の位置関係 平面と平面の位置関係 平面が動いてできる立体 立体の展開図 おうぎ形の弧の長さ おうぎ形の中心角 おうぎ形の利用 体積 応用問題 *「ページ表示」を「見開き」でご覧いただきますと問題とその答えが見�小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題2章 空間図形 46 132 学基本学習の基本 36 回転体の体積 問題 次の図形 を,直線¬ を軸として 1 回転させてできる立体の体積を求めよ。 ⑴ 長方形 ⑵ 直角三角形 ⑶ 半円 解 ⑴右の図のような円柱ができる。 ⑴ ⑵ ⑶ (∏×52)×10=250∏ (cm3) ⑵ 右の図のような円錐ができる。 1 3 ×(∏×32)×
とに関心をもち,意欲的に数学を問題解決に活用して考えたり判断したりしようとする。 (数学への関心・意欲・態度) (2)空間図形についての基礎的・基本的な知識及び技能を活用しながら,事象を見通しをもって 論理的に考察することができる。 (数学的な見方や考え方) (3)空間準的と思われる問題を紹介してみたいと思います.一般に,東大数学の空間図形の問題は トップ・バッターは,1991 年東大・文科の,正四角錐体と球との共通部分の体積を考え る問題です. 6・1正四角錐Vに対し,その底面上に中心をもち,そのすべての辺と接する球があ る.底面の1辺空間図形の総合問題1 立方体・直方体の対角線や、正四面体・正八面体の体積・表面積について学習します。 正四角錐 空間図形の総合問題1 空間図形の総合問題1 空間図形の総合問題1 空間図形の総合問題1 空間図形の総合問題1 空間図形の総合問題1
空間図形のまとめの問題です。1年生の数学の復習、定期テスト対策などにご利用ください。難しく感じる場合は空間図形の基本をもう一度復習していきましょう。空間図形の問題一覧 いろいろな立体 展開図と最短距離 直線や平面の平行線と垂直 回転体 立体の投影図 表面積 体積 球の体積と数学16章空間図形「立体の表面積と体積」<準備問題①> 組 番 名前 面積や体積の表し方や求め方について,次の問いに答えなさい。 (1)次のア~ウの面積を求めなさい。 (1マス1㎝の方眼で,イの縦の長さは05㎝とする。) ア イ ウ 1㎝2 体積8 不等式で表された立体の体積を求める問題です。 1. B (和歌山県立医大) (1) この領域と平面 との共通部分の面積 を求めよ. (2) この領域の体積を求めよ. 2. B (東海大) 連立不等式 を満たす点 全体からなる空間図形を とする.




数学中1 空間図形 写真の問題を教えてください 疑問点も書いてあります Clear




空間図形14 円すい台の体積 Youtube
体積や表面積を求める問題はよく目にすると思いますが その中でも円錐を取り上げた問題が一番よく出題されます。 なぜなら、円錐の問題には 空間図形の知識だけでなく、おうぎ形の知識も一緒に問うことができるからです。 出題者としては、この1問で2つの問いかけができるので中学レベル (一部解説動画つき)) 高校レベル (解説中学1年 空間図形 表面積や体積の求め方のポイントです。 代表的な三角柱,四角柱,円柱,球や半球などを取り上げて説明しますが、公式ではなく、求めるための手順を覚えるようにしましょう。 問題には公式が使えない立体が多く出てきますので、覚える




やや難しい立体の体積 Youtube




高校受験 数学テーマ別攻略 点が動く問題 日比谷高校のススメ
問題 体積の等しい立方体xと球yがあるとき, (1)yはxの頂点をいくつまで内部に含むことができるか? (2)yはxの辺をいくつまで内部に含むことができるか? (大阪大) 空間図形のシンプル難問正四面体の正射影の面積を最大化および最小化 おすすめ (問題文が特に第6章 空間図形 << L44 球の表面積と体積 の問題に戻る L45 切り取った立体の体積 の解答表示 >> 練習問題1 右図の12は、立方体をある平面で切り取って、その切り口に色をつけたものです。 このとき、以下の問いに答えなさい。 1 2点B,Dと中1数学 空間図形立体の体積と表面積の問題を練習できる教材プリント。無料ダウンロード・印刷できます。 数学の問題がわからなくて困ってます (空間図形) 題名の通り、下記の問題がわかりません。教えてください。 ここに、ab=ad=6cm,ae=7cmの直方体abcdefghがある。面abcdにおいて



立体の表面積と体積 数学の要点まとめ 練習問題一覧




立体の体積 無料で使える中学学習プリント
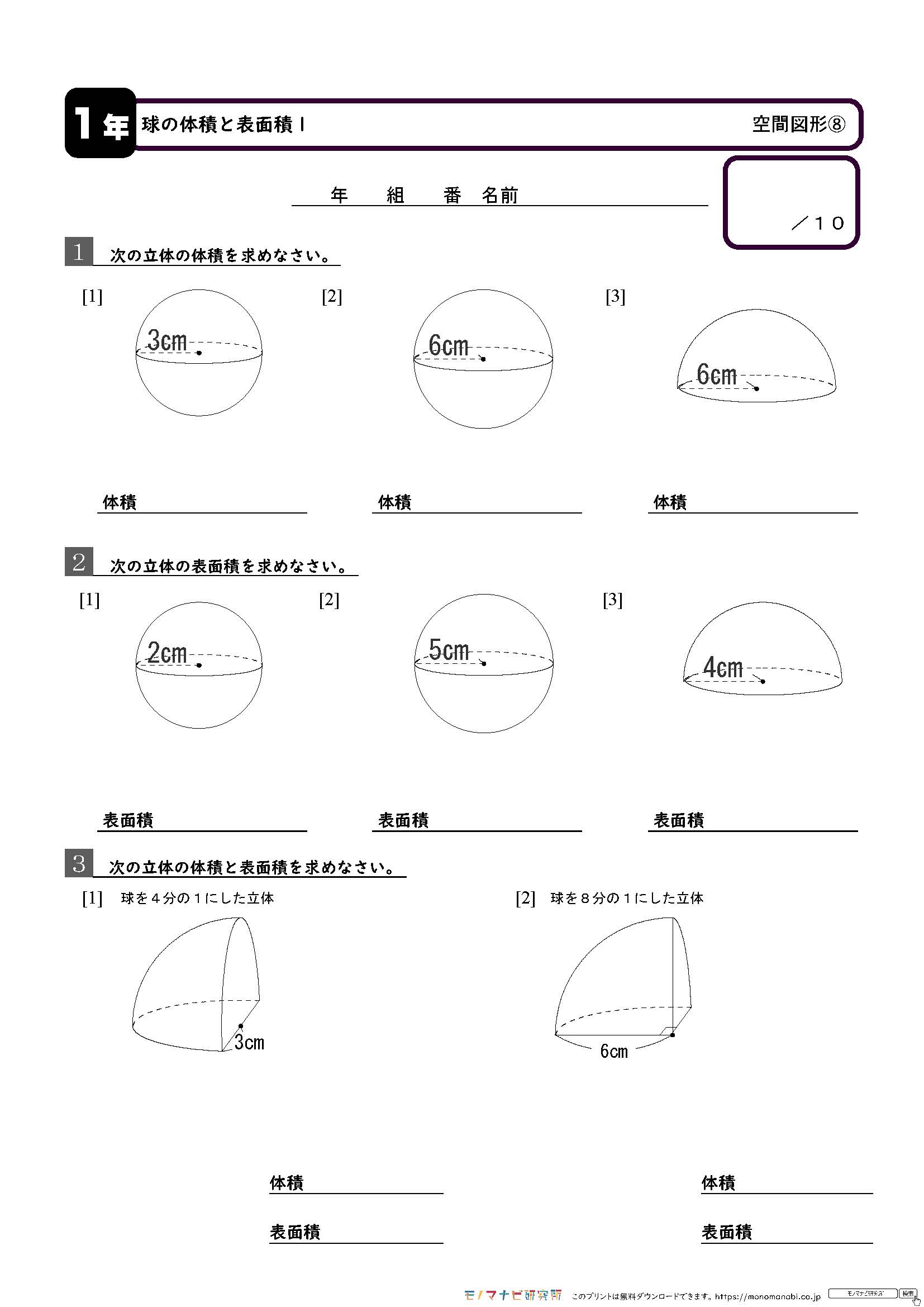
6空間図形 問題 円錐の体積は,円柱の体積の 倍になったね。 すい 3 だから,円柱の容器の水は,円錐の容器のちょうど 3杯分になるね。 ばい 1年生 6 空間図形 知識ヹ技能の習得を図る問題解答 年 組 号 氏名 全国学力ヹ学習状況調査④ A問題 1 H 年 組 号 氏名 1年生 6 空間図形 年 組 号6空間図形 問題 下の図のような半径が3cm の球があります。この球の表面積と体積を求めなさい。 円周率をπとする。 〔表面積〕 解答 〔体積〕 解答 3cm 10cm 5cm 4cm 中学校数学 第1学年 6空間図形 解答例 中学校 年 組 号 氏名 1年生 6 空間図形 1年生 6 空間図形 知識ヹ技能の習得を中学1年生 数学 空間図形立体の体積と表面積 練習プリント 無料ダウンロード・印刷 中1数学 空間図形立体の体積と表面積の問題を練習できる教材プリント。無料ダウンロード・印刷できます。




中学数学 空間図形 体積の問題のコツ




立体の表面積と体積 数学の要点まとめ 練習問題一覧
空間図形の面積と表面積の問題です。 簡単な図形で物足りなければ、どんどん複雑な図形に挑戦してみてください。 夢を叶える塾 数学を通して夢を叶える力を育む米沢市の学習塾 フォローする 夢を叶える塾 簡単なご案内; 空間図形と 積分 についてはかなり多く扱ってきました。 どれも一般に難問とされていますが、ポイントさえ抑えれば、簡単に解くことができます。 下の問題も、余裕のある方はチャレンジしてみてください。 四角錐と円柱、求積の基本 難関大学への空間図形を見取図、 展開図、投影図によ って適切に表現し、 図形の計量をしたり するなど、技能を身 に付けている。 空間図形についての 性質や関係、空間に おける図形の位置関 係などを理解し、知 識を身に付けてい る。 学 習 活 動 に 即 し た 具 体



毎日問題を解こう 18 苦手な数学を簡単に



無料 中1数学 基本問題 解答プリント 空間図形5 立体の表面積 142
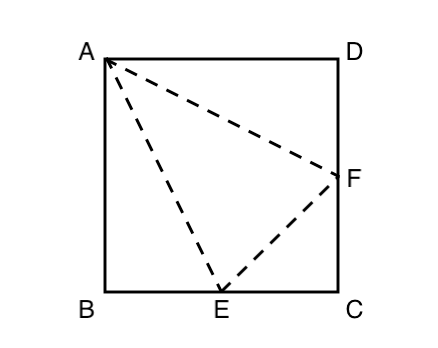
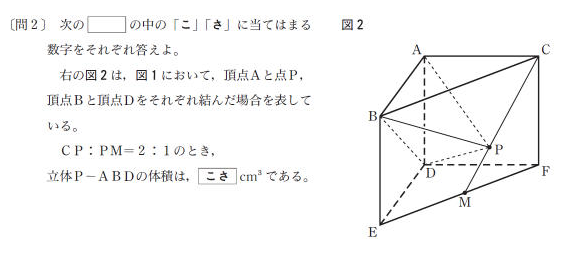
空間図形 (発展) 図は一辺12㎝の立方体である。 AP=3㎝、BQ=7㎝とする。 D,P,Qを通る平面でこの立方体を切ったときの切り口をDPQSとする。 (1) CS の長さを求めよ。 (2) 切断してできる立体のうち頂点Bを含むほうの立体の体積を求めよ。 図のような1辺6cmの立方これは東大の空間図形の体積の問題の解き方によく使う考え方が勉強できてええ問題やな。 東大だけじゃなくても役立つと思うわ、 東京大学の入試の数学の過去問の解説 Tweet 関連記事 東京大学18年度理系第6問、空間図形の体積の問題の解説 東京大学13年度理系第4問の確率、ベクトルのいが,「空間図形」に関する問題のうち角柱, 円錐などの表面積と体積を求める問題の通過 率が他の問題より低く,作図問題では通過率 が他の問題より高い傾向がある。」との調査 報告がある。この調査結果から図形領域にお いて空間図形についての




三平方の定理を使った空間図形の問題で質問です ウ の問題が分かりません Clear



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
空間図形に関する教育の内容と問題点、さらに今回制作したソフトの内容である、立方 体切断に関する内容と問題点について述べ、それらを考察する。 221 文部科学省の学習指導要領とその考察相似と面積比,体積比を絡ませた良い練習問題。 ・ポンデリング空間図形(★★★★☆)(17年度熊本県) 図が可愛らしい問題。 ・超楽しい空間図形(一部中1でも解ける)(★★★★☆)(年度立川高校) とてもとてもきれいな問題。入試数学コンテスト 正三角形の面積,正四面体の体積を求める公式 (i)1辺の長さが a a a の正三角形の面積 S S S は, S = 3 4 a 2 S=\dfrac{\sqrt{3}}{4}a^2 S = 4 3 a 2 (ii)1辺の長さが a a a の正四面体の体積 V V V は, V = 2 12 a 3 V=\dfrac{\sqrt{2}}{12}a^3 V = 12 2 a



空間図形



モノマナビ研究所
数学IA空間図形の応用問題茨城大・大阪市立大 前回に引き続き,三角比を利用して空間図形の問題を解く方法について説明します。 空間図形の問題では,体積を求める問題が多く出題されるため,様々な問題を解いて慣れておくことが中学数学 空間図形 トップページ > 中学1年生 > 空間図形 2年生問題集 ( excel 利用) が完成しましたので、よろしければご利用くださいね (全1539問) ( 有料 )。 1年生問題集は引き続き ( 無料 )です → ダウンロードページへ 中学1年生 中学2年生 課程へ空間図形1 次の問に答えよ 。 (1) 立方体や、直方体のように平面だけで囲まれた立体を何というか。 (2) (1)のうちどの面もみな合同な正多角形で、どの頂点にも面が同じ数だけ集まっているものを何とい



無料 中1数学 基本問題 解答プリント 空間図形6 立体の体積 143




この問題の解き方が分かりません Clear



展開図から立体の体積を求める 三角錐の問題 苦手な数学を簡単に




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト



Math 空間図形と相似 面積比 体積比 発展問題 働きアリ
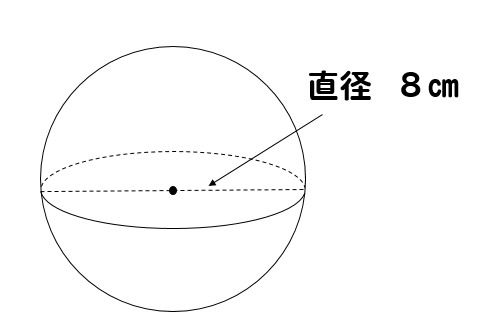



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ



中学数学の空間図形の問題が分かりません 立方体の体積から 立体p Yahoo 知恵袋




この問題を 水面が上昇した分を鉄球の体積 水槽の底面積で求めて 13センチから引くと Clear




公立高校入試 数学の勉強法 中3の夏以降にやることのおすすめ勉強法 コツまとめ 演習問題も充実 スタディサプリ中学講座



無料 中1数学 テスト対策問題 解答プリント 128 空間図形 立体 面積 体積
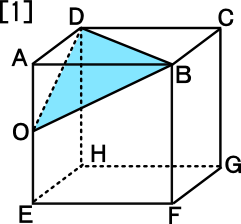



中学1年数学練習問題 空間図形 切り取った立体の体積の問題




中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
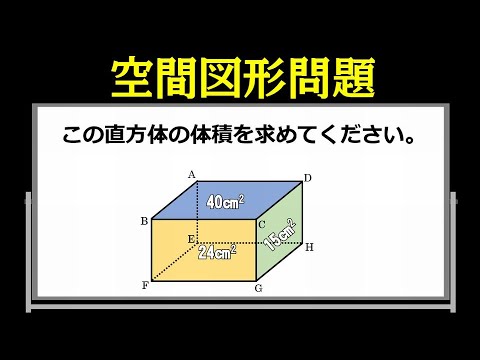



空間図形問題 気づけば解ける立体の問題です あなたはどう解きますか Youtube




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
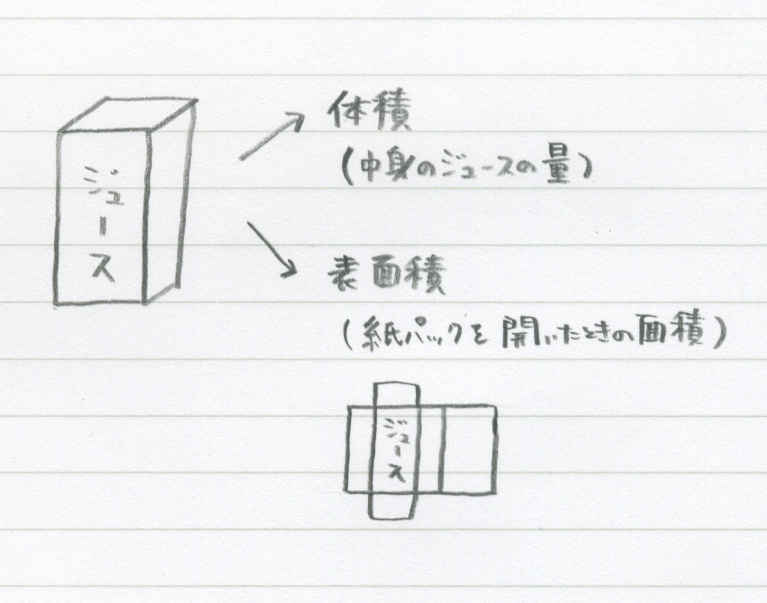



14 1 空間図形 体積 勉強できようサイト




角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun



無料 中1数学 基本解説 問題プリント 空間図形5 立体の体積 143
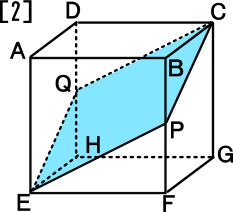



中学1年数学練習問題 空間図形 切り取った立体の体積の問題
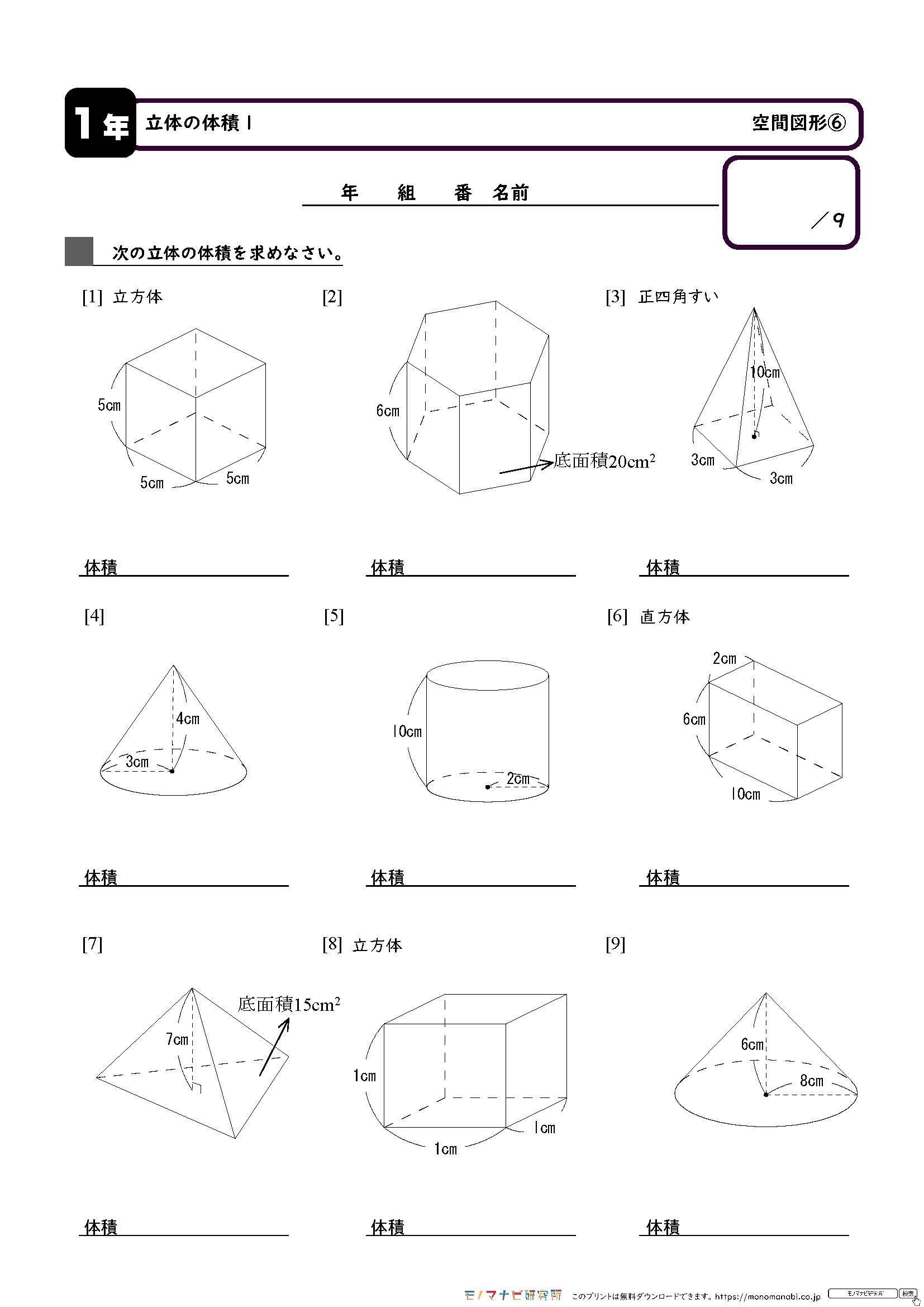



モノマナビ研究所
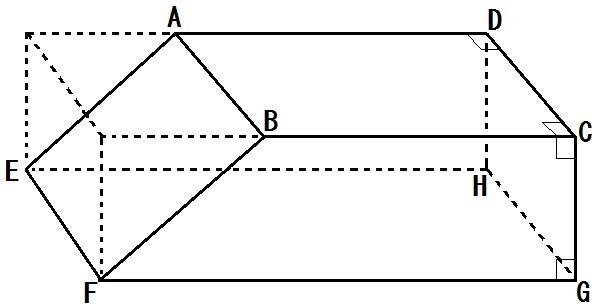



中学数学 空間図形 体積の問題のコツ




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学




21年大阪府c 相似と面積比 体積比の練習 高校入試 数学 良問 難問
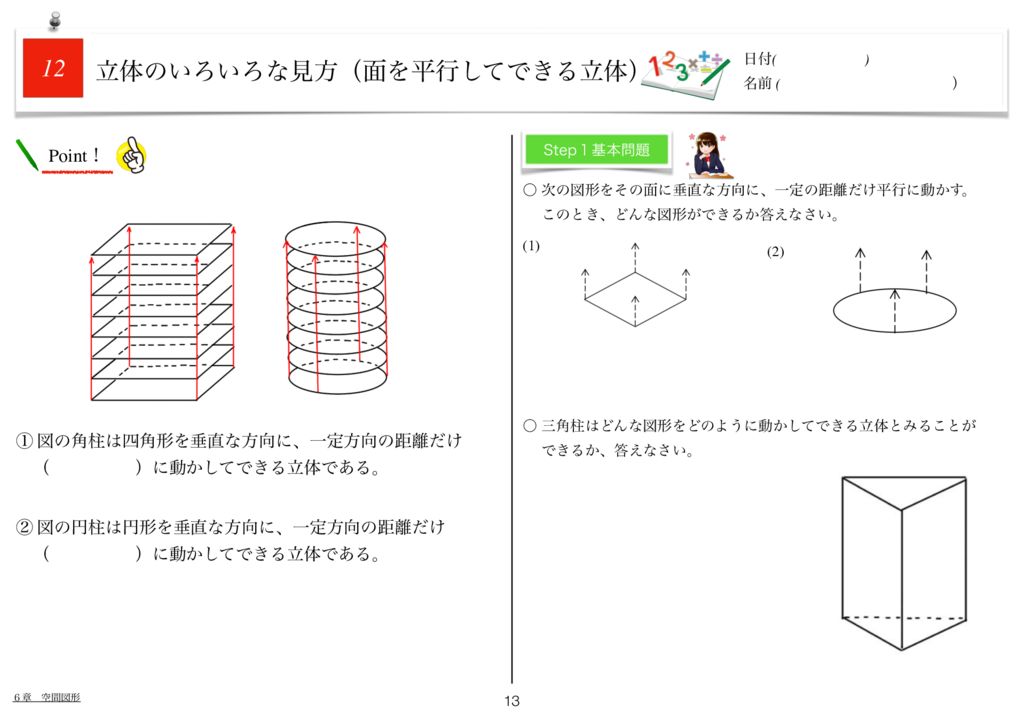



世界一わかりやすい数学問題集中1 6章 空間図形



空間図形 数スタ



身近な数学 空間図形 きのこたけのこの体積比べ
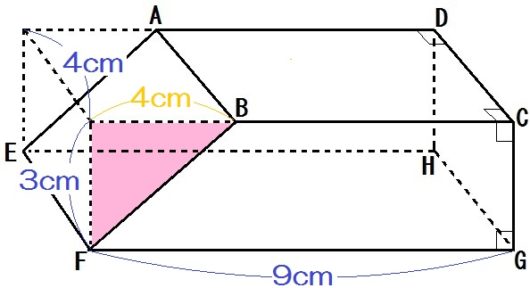



中学数学 空間図形 体積の問題のコツ




高校受験 入試 新潟県 数学 空間図形の問題 相似って便利ね 艸 オンライン授業 Youtube



空間図形 京極一樹の数学塾




立方体と正八面体の体積比 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください
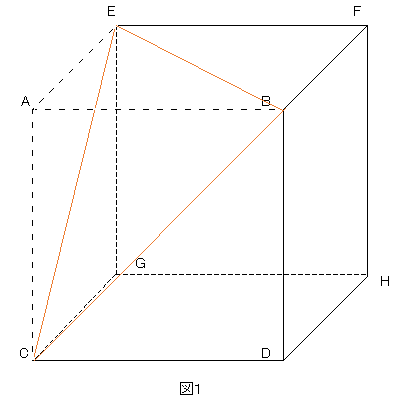



空間図形 練習問題 4 ネット塾




空間図形 線分を延長して相似な錐体を作って体積を求める問題 みみずく戦略室



中1の空間図形の問題なのですが球がきっちり入る1辺の長さが3 の Yahoo 知恵袋
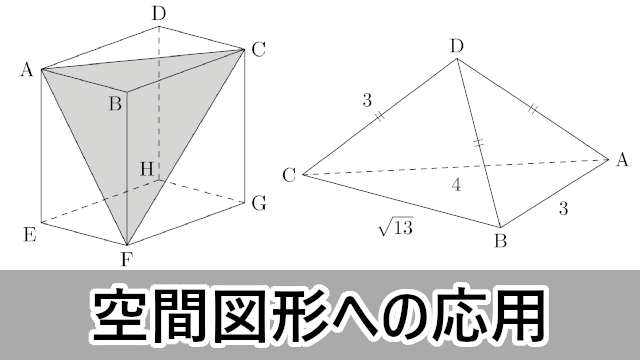



数学ia 空間図形の応用問題 広島工業大 東京慈恵会医科大 大学入試数学の考え方と解法



中1数学について質問です 画像見にくくてすみません 空間図形を切る単元の Yahoo 知恵袋




この問題の解き方が分かりません 答えは17分の7です Clear




立体の体積 無料で使える中学学習プリント



1




角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun
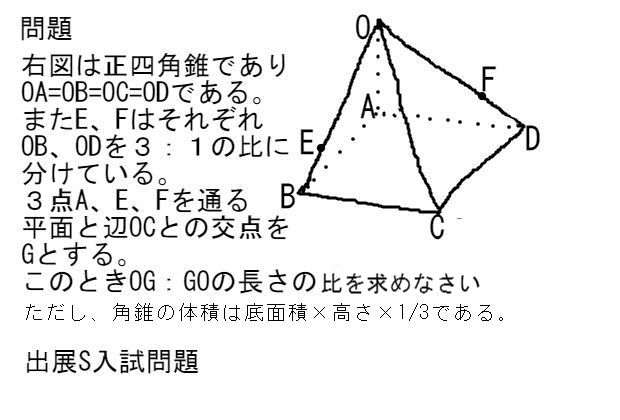



空間図形の超難問 チャレンジしておけばいつか役立つ総合問題 中学数学 理科 寺子屋塾の復習サイト
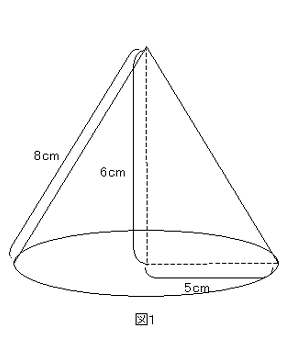



空間図形 練習問題 2 ネット塾




立体の体積 無料で使える中学学習プリント
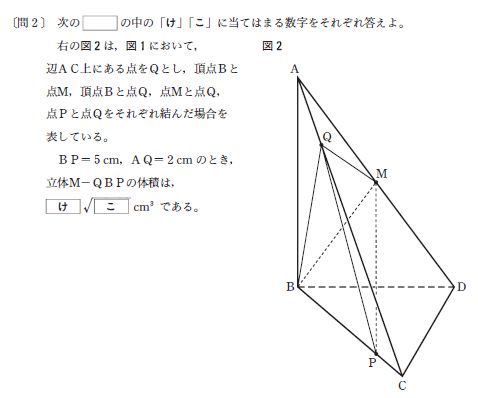



都立高校入試過去問解説 高さがわからない三角錐の体積を求めよう みみずく戦略室




角柱 円柱の表面積と体積の公式 数学fun
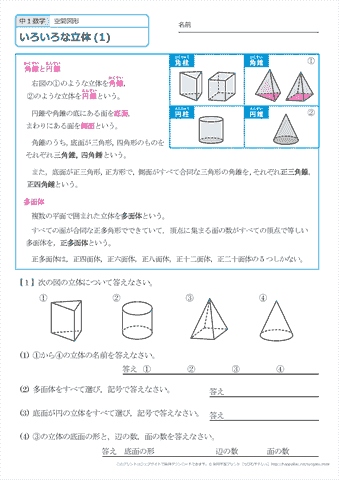



中学1年生 数学 空間図形 いろいろな立体 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



都立高校入試数学の空間図形問題が易化 来年度は難しくなるかも みみずく戦略室
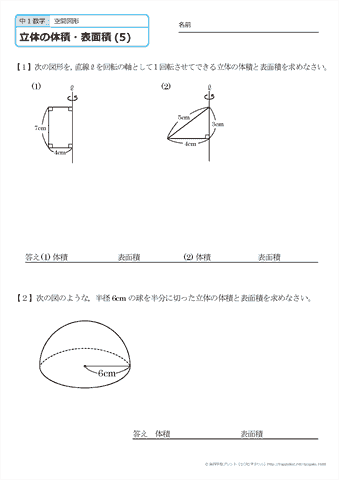



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
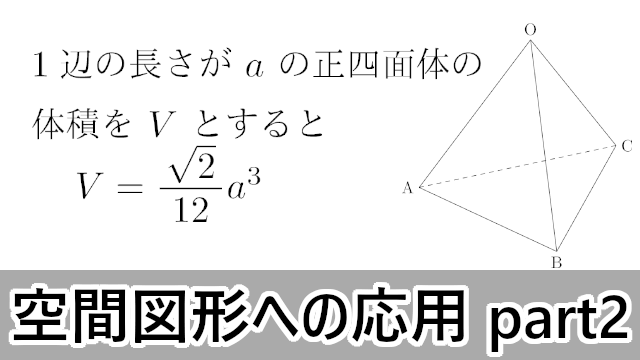



数学ia 空間図形の応用問題 茨城大 大阪市立大 大学入試数学の考え方と解法



空間図形 京極一樹の数学塾




世界一わかりやすい数学問題集中1 6章 空間図形



中一の数学の質問です 空間図形の問題です 三角柱abc Defの辺d Yahoo 知恵袋




球の表面積と体積の公式 数学fun



中1数学 発展 応用問題プリント 空間図形の立体の体積 143
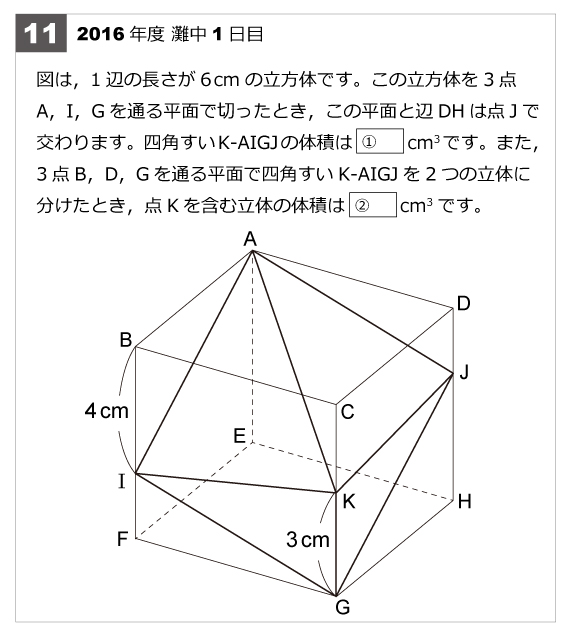



灘中解説速報 16年第11問 立体図形 難問 算数星人のweb問題集 中学受験算数の問題に挑戦




中1数学 立体の体積 練習編 映像授業のtry It トライイット



数塾ブログ 問題 点pが動く四角錐の体積を求める 空間図形




球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ
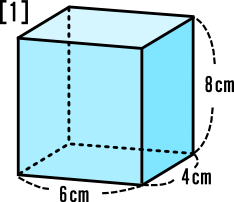



中学1年数学練習問題 立体 円柱 三角錘 四角錘等 の体積の問題



Q Tbn And9gcttyge0n1dey4bix07mlfzbh6wcasfwytbn5y1g0ze Kdv09o0c Usqp Cau




図形の性質 空間図形 5 3 2 さくらの個別指導 さくら教育研究所 Skredu



Search Q E4 B8 Ad E5 Ad A6 E6 95 B0 E5 Ad A6 E5 85 Ac E5 8f E5 8d B0 E5 Tbm Isch




空間図形15 断頭三角柱の体積 Youtube




角錐 円錐の体積と表面積の公式 数学fun
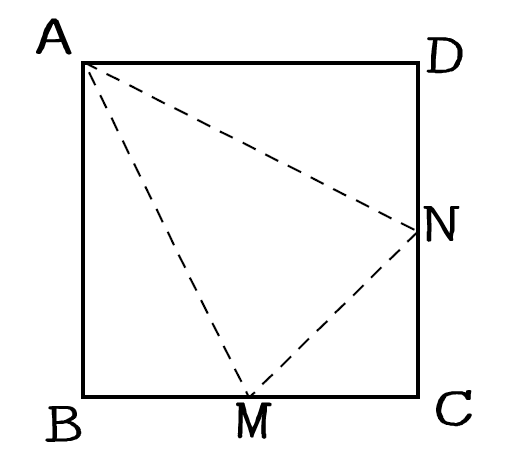



空間図形 発展




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学




日比谷高校のススメ



Q Tbn And9gcqbq1slf7zkihhbooec4pe8pu5gwh5eiw Hyepzmgbufcs Matk Usqp Cau




数学3 微積分 空間図形 立体の体積 さくらの個別指導 さくら教育研究所 Skredu



数学ia 空間図形の応用問題 関東学院大 摂南大 大学入試数学の考え方と解法
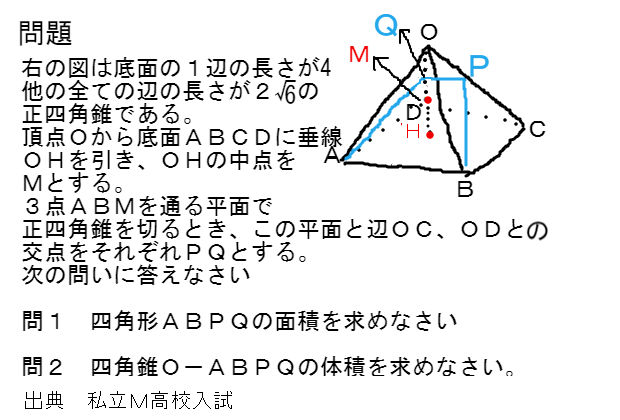



超難問 正四角錐の切断面の面積と切断立体の体積 中学数学 理科 寺子屋塾の復習サイト



Math 空間図形と相似 面積比 体積比 発展問題 働きアリ



無料 中1数学 基本問題 問題プリント 空間図形6 立体の体積 143



Mathematics 立体の切断 高校入試に出る難しい問題 働きアリ
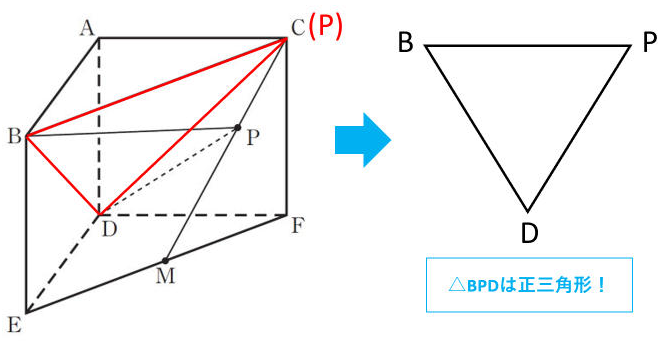



都立高校入試数学の空間図形問題が易化 来年度は難しくなるかも みみずく戦略室




中学一年数学 空間図形の発展問題について 画像にある応用問題 2問と 数学 教えて Goo




高校数学 3辺の長さが等しい 三脚型 四面体の体積 受験の月
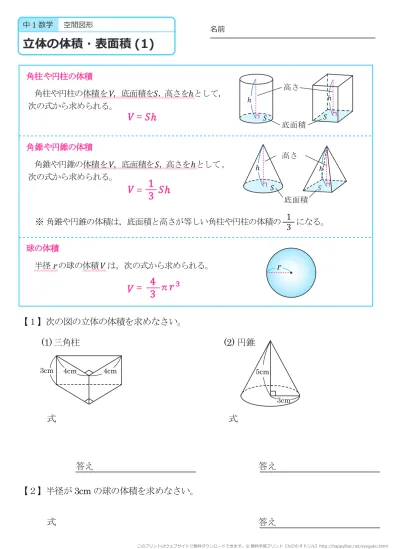



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 このページの答えのプリント 全部
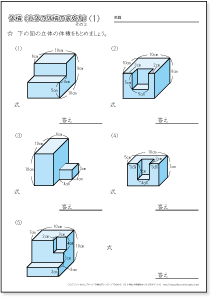



小学生の算数 図形 面積 体積 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 小学生




中学数学 空間図形 体積の問題のコツ



無料 中1数学 発展問題 解答プリント 空間図形6 立体の体積



数学i Aチェック リピート 第4章 2図形への応用 10 空間図形の体積 Pukiwiki




中1 数学 中1 立体の体積 Youtube
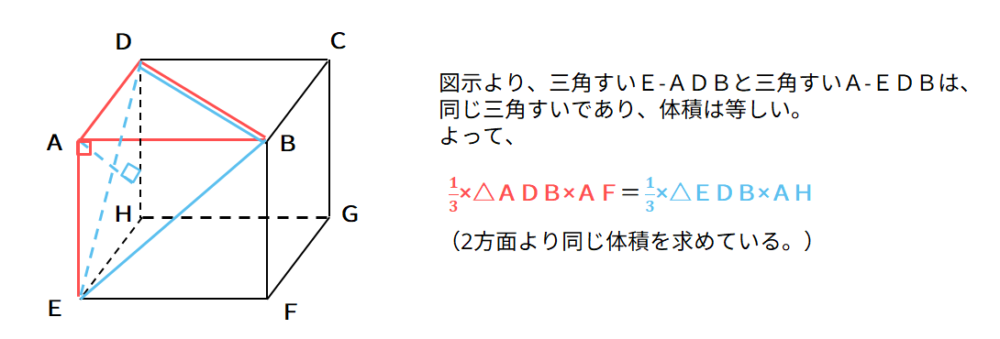



高校入試対策数学 空間図形と三平方の定理の対策問題 中学生勉強サイトあかね先生




2講 正多面体の体積 2節 空間図形 問題集 2章 図形の性質



中1数学 標準問題プリント 空間図形6 立体の体積 143



無料 中1数学 標準問題 解答プリント 143 空間図形6 立体の体積
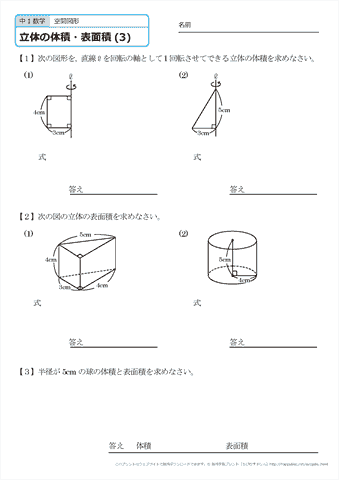



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



三角柱の体積の求め方 回転体の側面積の考え方 中学1年数学 空間図形




高校数学基本問題垂れ流し در توییتر 04 三角比と図形の測量 3 三角比と空間図形 錐体の体積と高さ




中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



0 件のコメント:
コメントを投稿