Hello School 算数 体積・表面積 練習問題 解答と解説 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。 ※特に指定がない場合、円周率は314とします。「柱」の体積は、(底面積)×(高さ) 今回は 「立体の体積」 を求めるよ。 体積の求め方は、「すい」と「柱」に関して2つの公式を覚えてしまおう。求める体積は =352cm 3 。 表面積 直方体2本の表面積は (4×4×212×4×4)×2 =448cm 2 。 重なっている表面積は 4×4×22×4×4=64cm 2 。 求める表面積は=384cm 2 。
6 17 第6章 空間図形立体の表面積と体積 円錐の表面積 ニュージーランド短期留学ダイアリー
立体の表面積と体積 問題
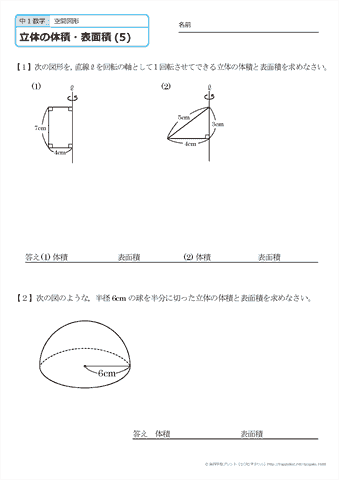
立体の表面積と体積 問題-みんなの算数オンライン 中学受験5年Unit9 1 立体図形1 体積と表面積 Author みんなの算数オンライン Keywords 体積,表面積,単位換算,角柱,円柱,角錐,円錐,展開図 Created Date AM10/9/19 回転体の体積、表面積の求め方 次の図形を直線を軸として1回転してできる回転体の体積、表面積を求めなさい。 正方形、長方形を回転させると円柱ができます。 つまり、上の図のような円柱の体積、表面積を求めれば良いということになります



立体 の 表面積 求め 方
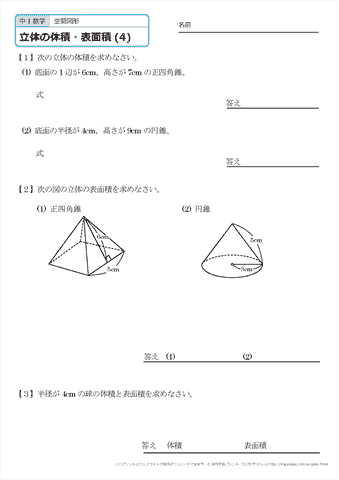
円錐の体積は、「底面積×高さ×1/3」で求めることができます。 ※円錐の体積がなぜ「底面積×高さ×1/3」で求められるのか? についての証明は特に学習しないので、本記事では円錐の体積の公式の証明は割愛します。 したがって、下の図のように、半径がr、高さがhである円錐の体積VをA = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体「表面積」 って分かるかな。 漢字のとおり、立体の 「表面の面積」 のことだよ。 底面や側面など、 すべての面の面積 を求めて、たし合わせよう。
8/9/19 立体の表面積の求め方 立体の表面積とは 立体の表面全体の面積のこと をいいます。 立体の表面積の公式も一応示しますが、考え方を理解することができていればわざわざ公式を覚える必要立体の表面積と体積 16c 立体の表面積と体積 中学1年の単元 こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積(表面積)を求める方法についてまとめています。 前回の記事(Part26)はこちら! 広義積分・ガウス積分についてまとめています。こ
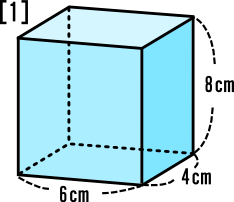
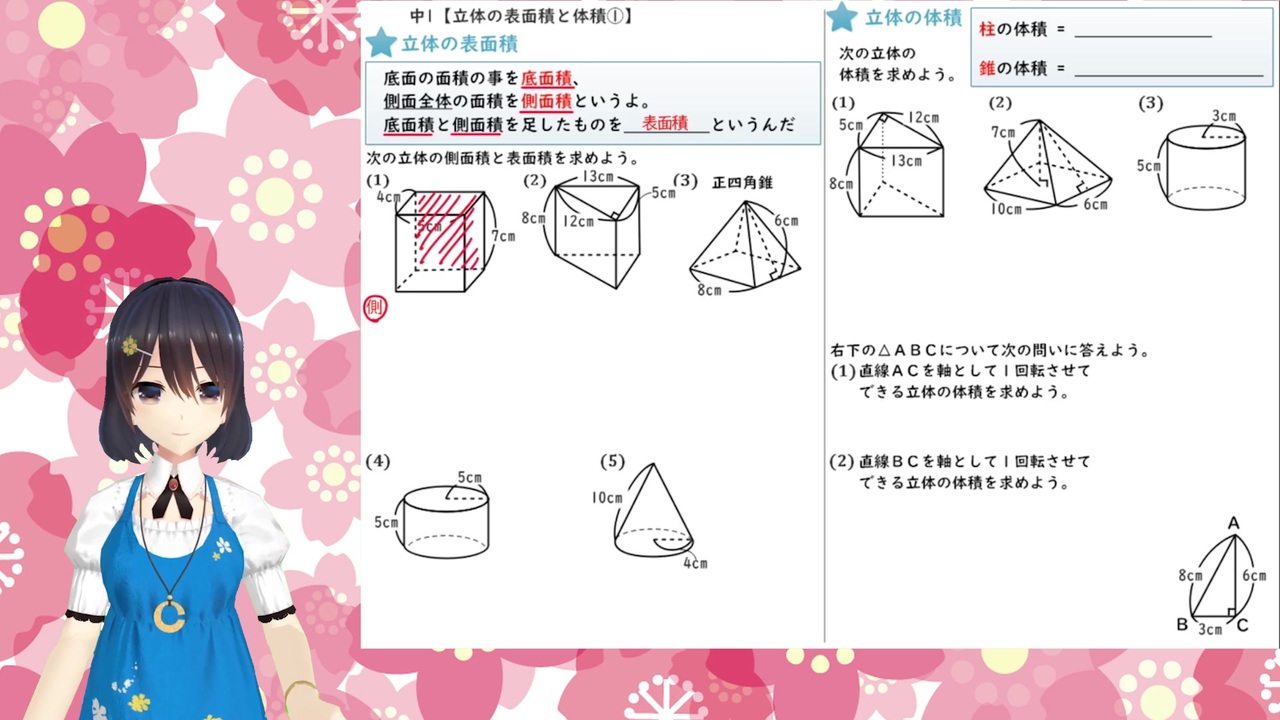
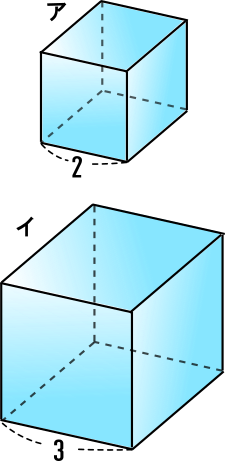
中学受験の算数・理科ヘクトパスカルによる四谷大塚予習シリーズ算数「立体図形の研究(体積と表面積)の問題」の手書き解説です。立方体から直方体をいくつか取り除いて,右の図の ような立体を作りました。これについて,次の問いに 答えなさい。 (1) この立体の体積は何cm3ですか。回転体の体積 下の図のような直角三角形abcで次のような二つの回転体をつくる。どちらの体積が大きいだろうか。 ア 直線abを軸として1回転させてできた立体 イ 直線acを軸として1回転させてできる立体 c b a 3㎝ 6㎝ c b a 3㎝ 6㎝ ア c a b 6㎝ 3㎝ イ4/8/21 (2)OH=18cm,AH=6cmとするとき、立体Rの体積を求めなさい。 相似な立体の表面積・体積の定期テスト過去問分析問題の解答 問1 (1)169=x135 9x=2160 x=240 (答え)240cm 2 (2)6427=192x 64x=5184 x=81 (答え)81cm 3 問2 (1) 1:4 (2) 立体の体積 =1/3×36×18 =216 求める体積R =216×19/27 =152 (答え)152cm 3



6 17 第6章 空間図形立体の表面積と体積 円錐の表面積 ニュージーランド短期留学ダイアリー




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
中学校1年生 *単元確認テスト* 3学期① 立体の表面積と体積 組 番 名 前 /10 1 次の文章の( )の中に、下の からあてはまる言葉を選び、文章を完成させなさい。 (1点×3) 立体のすべての面の面積の和を( 表面積 )という。動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru立体の体積、表面積 問題 ・・・ (む) は難しい問題です。 1 右図の四角錐の底面は1辺の長さ6 (cm)の正方形,側面は等しい辺の長さが2√7 (cm)の二等辺三角形です。 この四角錐の体積は (cm 3 ) ア= イ= この四角錐の表面積は (cm2) ウ= エ= オ= 2 右図は1辺の長さが6cmの正四面体です。



立体の表面積




球の体積と表面積 Youtube
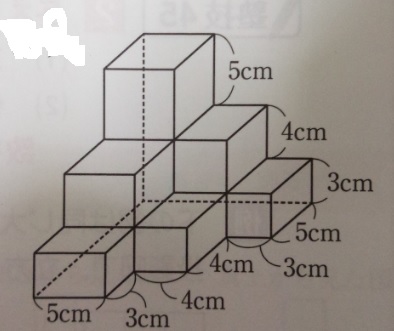
体積・表面積⑵ 角柱 15 ステップ5 複合図形の表面積 15 図の立体は、直方体を組み合わせてできた立体ですが、色のついた面 を底面とする柱と考えることができます。 ⑴ この柱の底面積は( )㎠です。 ⑵ この柱の底面のまわりの長さは( )㎝です。AB=3㎝、BC=4㎝、CA=5㎝、AD=10㎝である。 この三角柱の辺BE上にBP=6㎝となる点Pをとり、点A,P,Fを通る平面でこの立体を2つに分けてできるそれぞれの立体の体積を求めよ。 A B C D E F P 図の直方体は AB=10cm, BC=4cm, BF=6cm である。 BQ=5cm, AP=1cm となる点P,Qをとり、D,P,Qを通る平面でこの直方体を2つに分ける。 2つに分けたそれぞれの立体の体積を求めよ。 A B C D E 積み重ねられた立体の体積:立体を段ごとに分解 最初は自分で図を描いてみても良いです。 125 260 180+108+45=333 125+260+333=125+593=718 答え)718cm 3 (2)この立体の表面積を求めなさい 積み重ねられた立体の表面積:(前+右+上)×2 97+97+111




立体の表面積と体積 の問題のわからないを5分で解決 映像授業のtry It トライイット




円柱を2つ重ねた立体の表面積の求め方 Qikeru 学びを楽しくわかりやすく
149 次の図のよ う な立体の体積と表面積を求めよ 。 ⑴ 半球 ⑵ 球の 1 4 ⑶ 半球と円柱を組み合わせた立体 学基本学習の基本 35 球の体積と表面積 半径 r の球の体積をV,表面積をSとすると 立体の表面積を聞かれたら、展開図を書こう! ということ。展開図さえ書けば、そこに見えるのは長方形であったり、円であったり。ただの平面図形です。 それらの面積を1つ1つ出してから足し合わせるだけ。シンプルです。 立体の体積 表面積の後は立方体の辺の長さから体積と表面積を計算します。 立方体の辺の長さ 立方体の辺の長さ 立方体の体積から辺の長さと表面積を計算します。 直方体の体積 直方体の体積 直方体の三辺の長さから体積と表面積を計算します。 四面体の体積 四面体の体積



中学1年数学練習問題 立体 円柱 三角柱 四角錘等 の表面積の問題



1
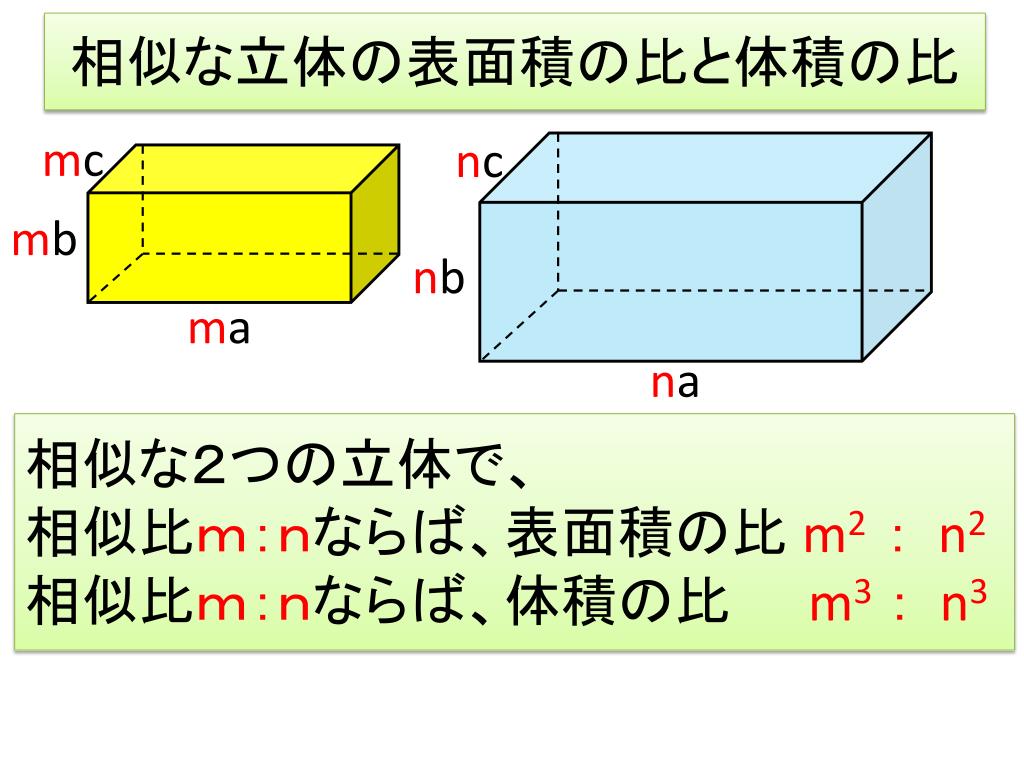
・ 立体の表面積や体積を、相似な立体の相似比と表面積の比、体積の比の関係を使って 求めることができる。 ・ 立体の相似の意味と性質、相似比と表面積の比、体積の比の関係を理解する。おうぎ形,立体の表面積・体積 ⑥ 次のおうぎ形の弧の長さと面積を求めな さい。 (1) 半径6cm,中心角60°のおうぎ形 次のおうぎ形の中心角の大きさを求めな さい。 (1) 半径5cm,弧の長さ4,cmのおうぎ形 (2) 半径cm,弧の長さ8,cmのおうぎ形 面積①半径 の球の体積 を求める式。 4# ②半径 の球の表面積 を求める式。 32 次の球の表面積と体積を求めなさい。 cm 表面積: 体積: cm 表面積: 体積: 右の図は、半径が cmの球を、中心を通る平面で切って できた立体である。このとき次の 問いに答えなさい。



立体の表面積と体積 中学受験 算数入試問題 どう解く 中学受験算数



無料 中1数学 基本問題 問題プリント 空間図形6 立体の体積 143
29/3/21 A 体積32π($cm^3$)・表面積40π($cm^2$) 円柱の体積の求め方は「底面積 × 高さ」でしたね。 また円の求め方は「半径 × 半径 × π」なので、式は 2 × 2 × π × 8 = 32π 体積は32π($cm^3$)となります。 次に、円柱の表面積の求め方は「底面積 × 2 側面積」なので、式は「4π × 2 側面積」。全体の体積 1344cm 3 672cm 3 =16cm 3 (解2) 直方体Cの体積 6cm×(14cm7cm)×16cm=672cm 3 直方体Dの体積 (12cm6cm)×14cm×16cm=1344cm 3 全体の体積 672cm 3 1344cm 3 =16cm 3 (解3) 立体の底面積 12cm×(14cm7cm)(12cm6cm)×7cm=126c㎡ 立体の体積 126c㎡×16cm=16cm 3 (解4) 大きな直方公式計算 平面図形の面積(a),周長(l)および重心位置(g) p11 平面図形の性質 p12 立体の体積(v),表面積(s)または側面積(f)および重心位置(g) p12
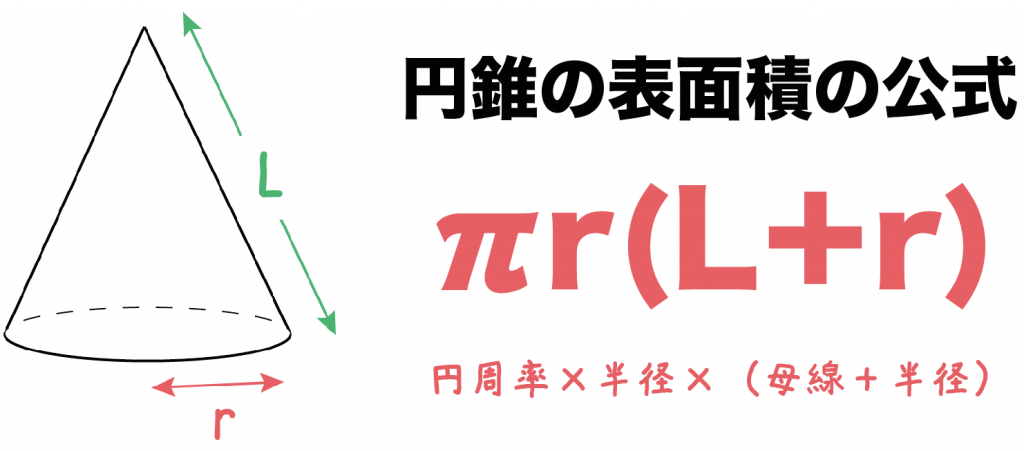



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



6 3 複雑な図形を1回転させてできる立体の体積と表面積を求めるには さんすうがく パート 2
立方体の12の辺の長さは等しく、これを $a$ とします。立方体の表面積 $S$ は、次の式で求められます。 立方体の表面積 \begin{align*} V = 6a^2 \end{align*} 表面積 = 一辺 × 一辺 × 6立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V (x) で表し, x における断面積を S (x) とおきます.一番大きいと思う立体を、各自で作る。 展開図を準備しておく) グループで城の大きさ比べをする。 分解した立体で形を整理する。 分類(柱体・すい体)して、求め方を考える。 1)表面積では 2)体積




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
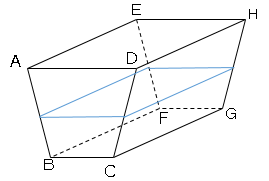



立体の表面積と体積46 数学の要点まとめ 練習問題一覧
§1立体の表面積(2時間) 空間図形の表面積・側面席・底面積がどの面の面積かを理解する。 円柱、柱体、角錐の側面積と表面積が算出できる。 知-④ 技-④ 円錐の表面積が算出できる。 円錐の母線と底面の半径について考察できる。 技-④




この図形を直線lを軸として一回転させてできる立体の表面積と体積を求める問題です Clear




中1 中1 数学まとめ 立体の体積や表面積など 中学生 数学のノート Clear
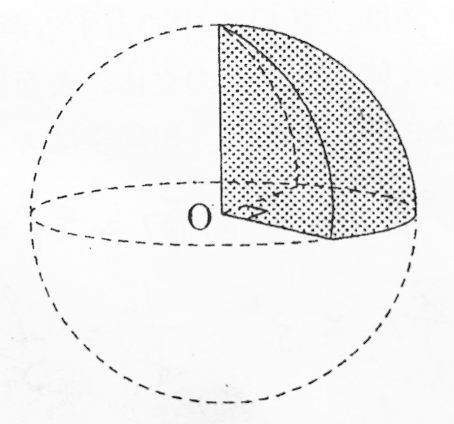



球の問題 苦手な数学を簡単に




円錐の表面積 Youtube




球の体積と表面積 公式と計算問題と証明 Irohabook




球の表面積と体積の公式 数学fun




中1 数学 空間図形12 立体の表面積 18分 Youtube



6 13 第6章 空間図形立体の表面積と体積 角柱や円柱の体積 ニュージーランド短期留学ダイアリー



高校入試 英語 数学 学習 立体の表面積と体積



立体の表面積と体積についてです 写真にある投影図で表された立体 Yahoo 知恵袋



無料 中1数学 標準問題 解答プリント 143 空間図形6 立体の体積
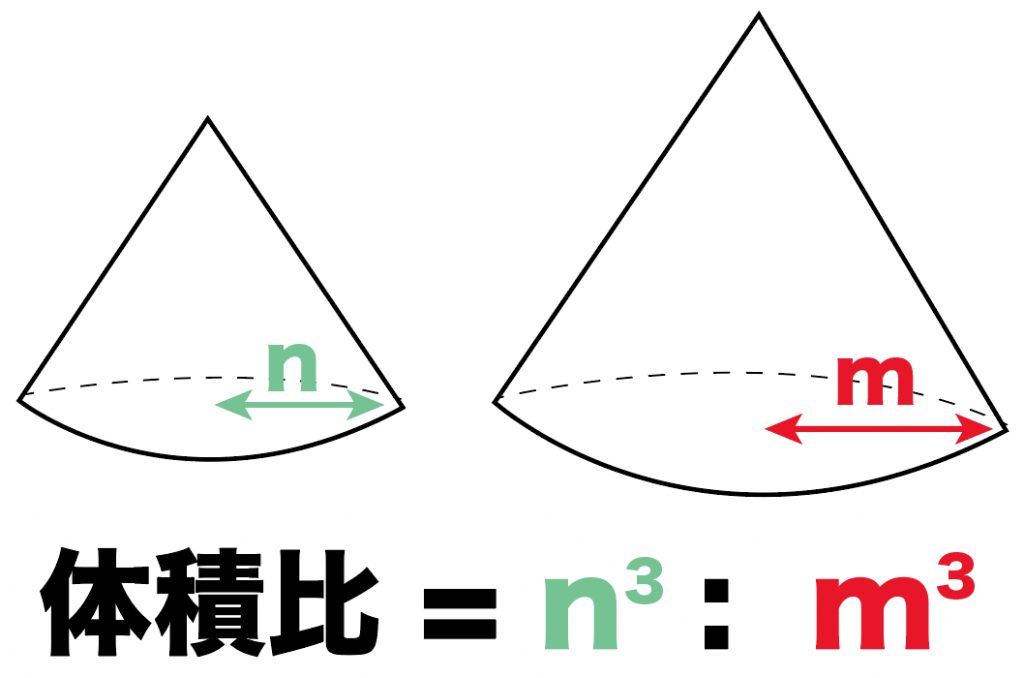



3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく
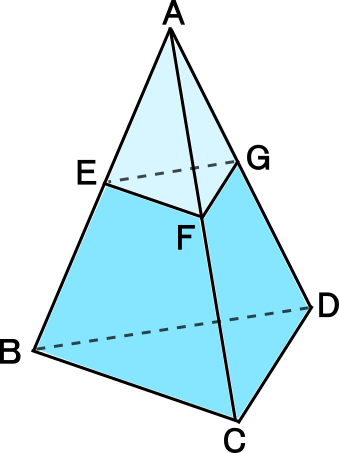



中学3年数学練習問題 図形と相似 相似な立体の表面積と体積の比




中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




実際にやってみました 聖徳大学附属取手聖徳女子中学校 高等学校




角柱 円柱の表面積と体積の公式 数学fun



中学数学acを軸として一回転してできる立体の表面積と体積を求め Yahoo 知恵袋




中学生 立体の表面積と体積のノート一覧 Clear




2 Abcd Ad 1 A Descubre Como Resolverlo En Qanda



立体 の 表面積 求め 方




Ad B 5cm cm C Descubre Como Resolverlo En Qanda
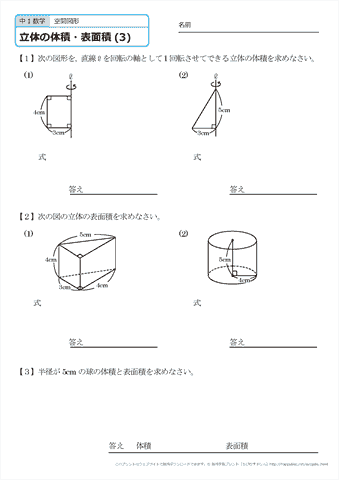



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Studydoctor柱体や角錐の表面積の求め方 中学1年数学 Studydoctor




数学 中学1年 立体の表面積と体積 ニコニコ動画




球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




表面積の求め方 計算公式一覧




立体の表面積と体積 の問題のわからないを5分で解決 映像授業のtry It トライイット




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




中3 三年数学 立体の表面積の比と体積の比 中学生 数学のノート Clear




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu




5章3節2 相似な立体の表面積や体積の比 数学のすすめ




Lihat Cara Penyelesaian Di Qanda



1
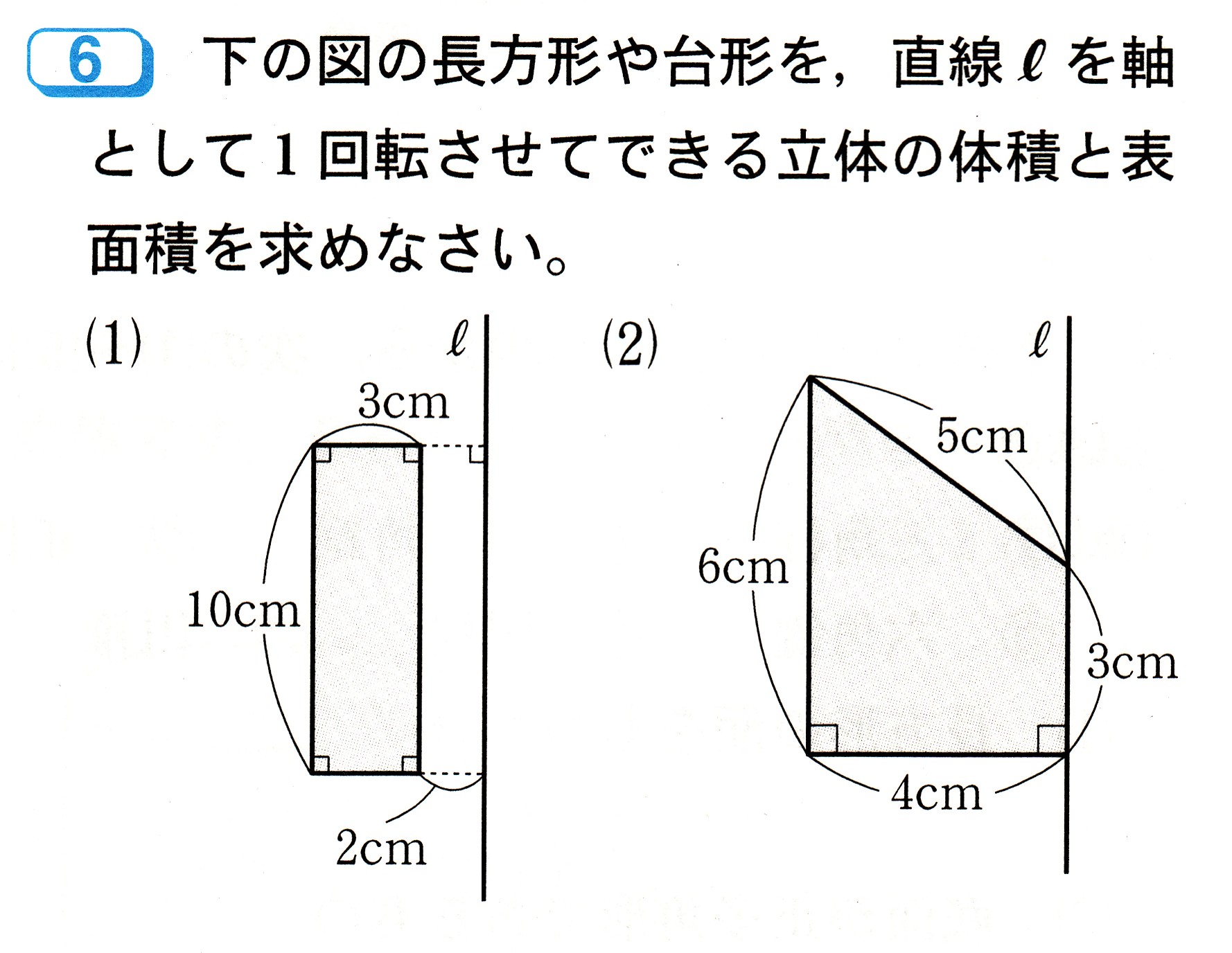



中学1年数学 立体の表面積と体積 確認問題6 あんのん塾




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム




球の表面積と体積の公式 数学fun




中1 数学 中1 立体の表面積 Youtube




立体の表面積と体積 の問題のわからないを5分で解決 映像授業のtry It トライイット




10 面積比 体積比 球の表面積と体積



5 5 複雑な立体の表面積と面積を求めるには さんすうがく




Sqrt3 6cm 0 Descubre Como Resolverlo En Qanda
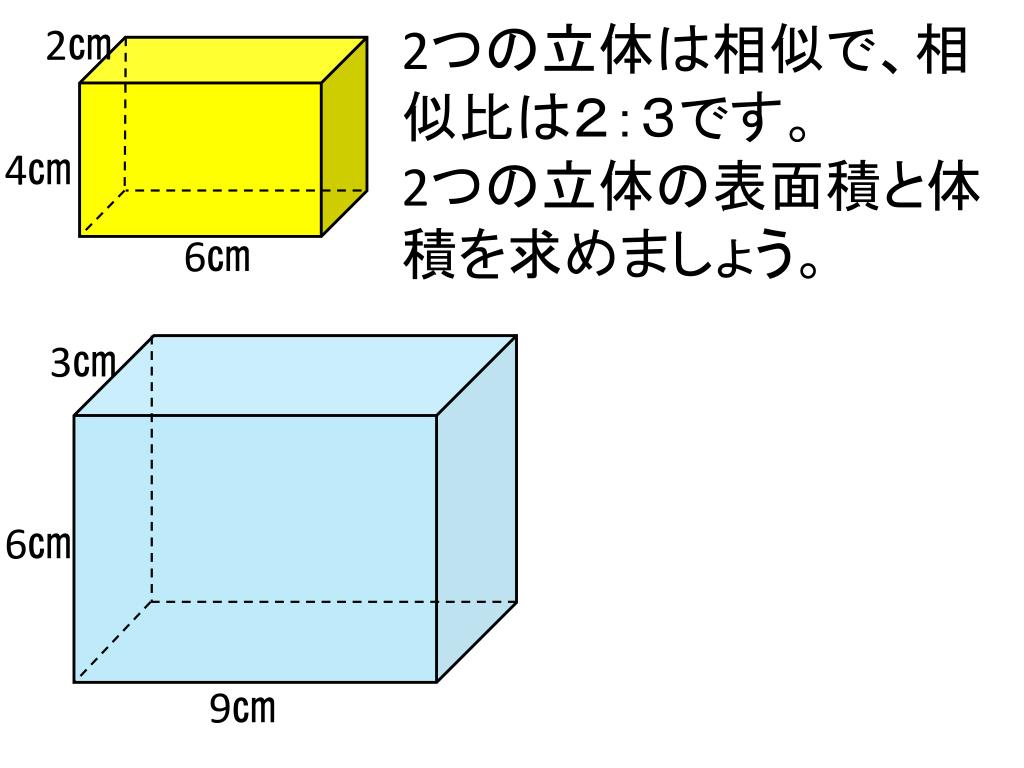



Ppt 相似な立体の表面積 体積 Powerpoint Presentation Free Download Id




角柱 円柱の表面積と体積の公式 数学fun




角錐 円錐の体積と表面積の公式 数学fun




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



立体の表面積と体積 わかる数学




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



高校入試 英語 数学 学習 立体の表面積と体積




三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学




中1 数学中2 立体の体積と表面積 公式 中学生 数学のノート Clear




角錐 円錐の体積と表面積の公式 数学fun




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン



Ppt 相似な立体の表面積 体積 Powerpoint Presentation Free Download Id



1




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




立体の表面積と体積 数学の要点まとめ 練習問題一覧
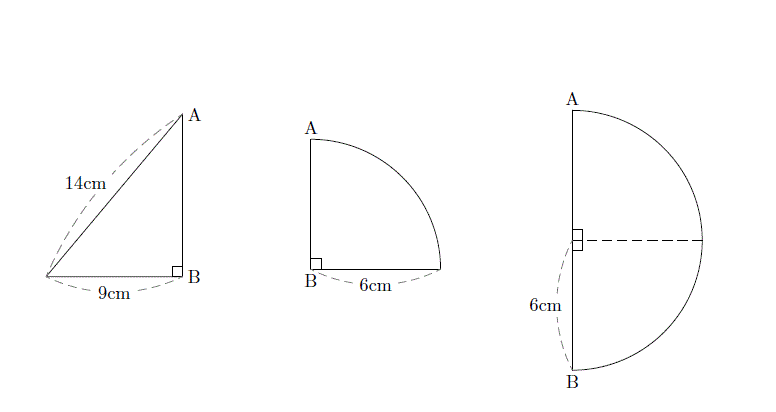



かみのドリル 立体の体積と表面積 回転




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ




簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ




体積 表面積



数学 中学1年 立体の表面積と体積 ニコニコ動画




表面積と体積の比の問題 立体の相似比を出すのが一番最初だ 中学や高校の数学の計算問題




中1 回転体の表面積と体積についてです 右の画像が模範解答です Clear
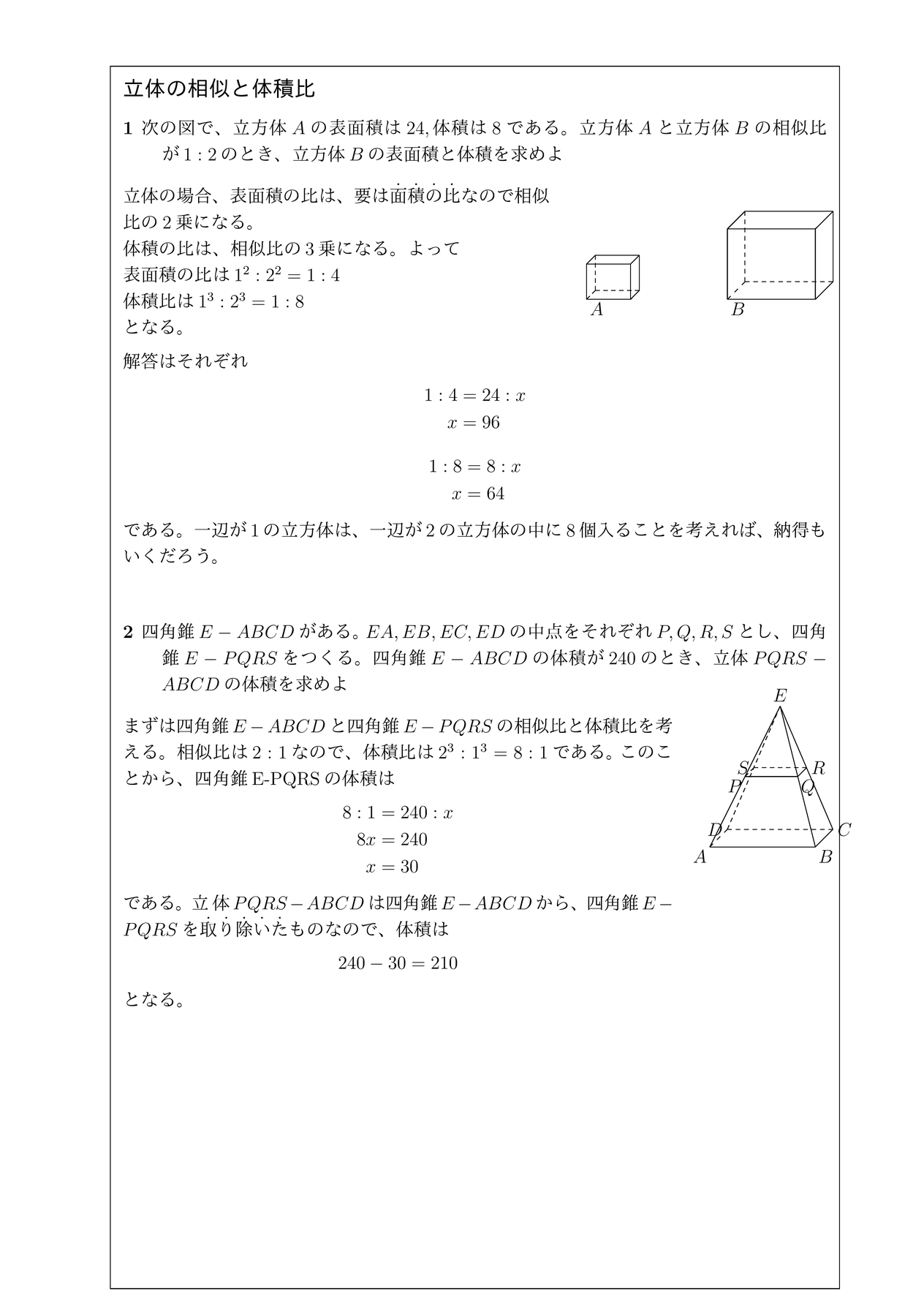



立体の相似と表面積比 体積比 チーム エン




表面積の求め方 計算公式一覧



積み重ねられた立体 表面積と体積 中学受験 塾なし の勉強法



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



1




球の表面積と体積の公式 数学fun




5章3節2 相似な立体の表面積や体積の比 数学のすすめ




中1 数学 6 5 球の体積 表面積 Youtube




立体の表面積と体積 の勉強法のわからないを5分で解決 映像授業のtry It トライイット



この問図形の表面積と体積を教えてください 上の円錐と円柱 Yahoo 知恵袋



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




Hd限定円錐 体積 の 求め 方 ページを着色するだけ




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン



中学3年数学練習問題 相似な立体の表面積と体積の比 図形と相似




中1数学31 立体の表面積と体積 Youtube




Descubre Como Resolverlo En Qanda



立体 の 表面積 求め 方




円柱の表面積と体積を求める公式 具体例で学ぶ数学




中1 数学 中1 立体の体積 Youtube
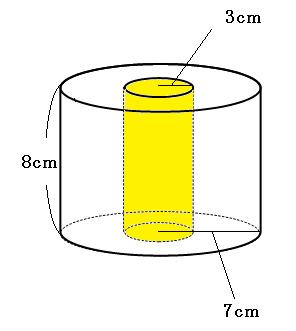



立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか
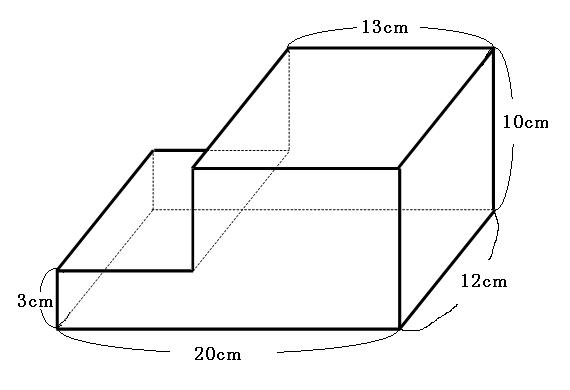



立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか
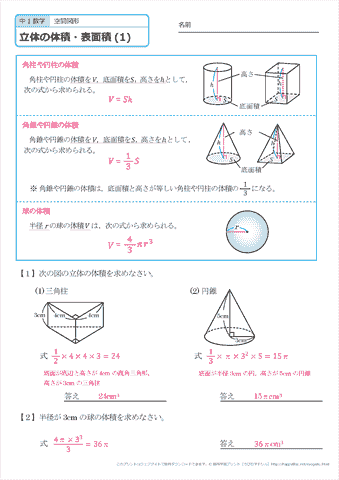



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト




9 1 115 Times21 Descubre Como Resolverlo En Qanda




Ppt 相似な立体の表面積 体積 Powerpoint Presentation Free Download Id



0 件のコメント:
コメントを投稿